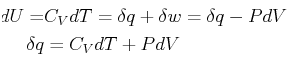Next: Homogeneous and Heterogeneous Linear ODES
Up: Lecture_20_web
Previous: Ordinary Differential Equations from Physical Models
Next: Homogeneous and Heterogeneous Linear ODES
Up: Lecture_20_web
Previous: Ordinary Differential Equations from Physical Models
Subsections
Exact Differential Forms
In classical thermodynamics for simple fluids, expressions such as
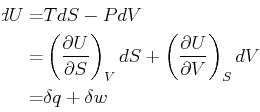 |
(20-8) |
represent the differential form of the combined first
and second laws of thermodynamics.
If 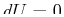 , meaning that the differential Eq. 20-8 is
evaluated on a surface for which internal energy
is constant,
, meaning that the differential Eq. 20-8 is
evaluated on a surface for which internal energy
is constant,
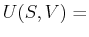 const
, then the
above equation becomes a differential form
const
, then the
above equation becomes a differential form
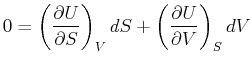 |
(20-9) |
This equation expresses a relation between changes in
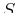 and changes in
and changes in 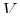 that are necessary to remain on
the surface
that are necessary to remain on
the surface
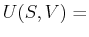 const
.
const
.
Suppose the situation is turned around and you are given the
first-order ODE
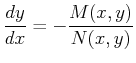 |
(20-10) |
which can be written as the differential form
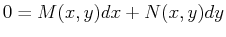 |
(20-11) |
Is there a function
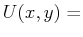 const
or, equivalently,
is it possible to find a curve represented by
const
or, equivalently,
is it possible to find a curve represented by
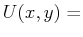 const
?
const
?
If such a curve exists then it depends only on one parameter, such
as arc-length, and on that curve 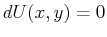 .
.
The answer is, ``Yes, such a function
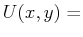 const
exists
if an only if
const
exists
if an only if 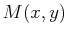 and
and 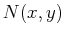 satisfy the Maxwell relations''
satisfy the Maxwell relations''
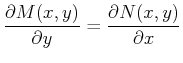 |
(20-12) |
Then if Eq. 20-12 holds, the differential form
Eq. 20-11 is called an exact differential and
a 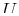 exists such that
exists such that
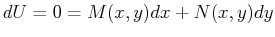 .
.
Integrating Factors and Thermodynamics
For fixed number of moles of ideal gas,
the internal energy is a function
of the temperature only,
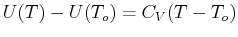 .
Consider the heat that is transfered to a gas that
changes it temperature and volume a very small amount:
.
Consider the heat that is transfered to a gas that
changes it temperature and volume a very small amount:
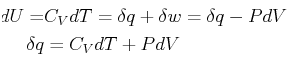 |
(20-13) |
Can a Heat Function
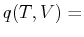 constant
be found?
constant
be found?
To answer this, apply Maxwell's relations.
© W. Craig Carter 2003-, Massachusetts Institute of Technology
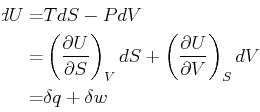
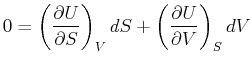
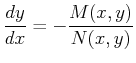
![]() .
.
![]() const
exists
if an only if
const
exists
if an only if ![]() and
and ![]() satisfy the Maxwell relations''
satisfy the Maxwell relations''
![]() .
Consider the heat that is transfered to a gas that
changes it temperature and volume a very small amount:
.
Consider the heat that is transfered to a gas that
changes it temperature and volume a very small amount: