In engineering and physics, modeling physical phenomena is the means by which technological and natural phenomena are understood and predicted. A model is an abstraction of a physical system, often with simplifying assumptions, into a mathematical framework. Every model should be verifiable by an experiment that, to the greatest extent possible, satisfies the approximations that were used to obtain the model.
In the context of modeling, differential equations appear frequently. Learning how to model new and interesting systems is a learned skill--it is best to learn by following a few examples. Grain growth provides some interesting modeling examples that result in first-order ODES.
In materials science and engineering, a grain usually refers a single element in an ensemble that comprises a polycrystal. In a single phase polycrystal, a grain is a contiguous region of material with the same crystallographic orientation. It is separated from other grains by grain boundaries where the crystallographic orientation changes abruptly.
A grain boundary contributes extra free energy to the entire system that is proportional to the grain boundary area. Thus, if the boundary can move to reduce the free energy it will.
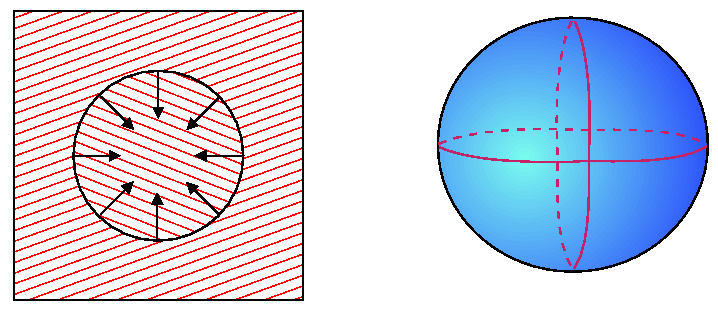
Consider simple, uniformly curved, isolated two- and three-dimensional grains.

A relevant question is ``how fast will a grain change its size assuming that grain boundary migration velocity is proportional to curvature?''
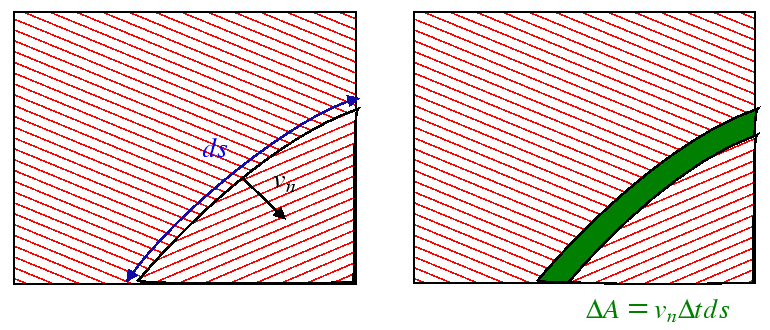
For the two-dimensional case, the rate of change of area can be formulated by considering the following illustration.
|
|
Because for a circle, the curvature is the same at each location on
the grain boundary, the curvature is uniform and
![]() .
Thus
.
Thus
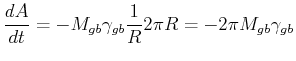 |
(20-1) |
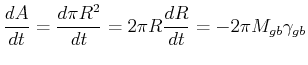 |
(20-2) |
| (20-3) |
For a spherical grain, the change in volume ![]() due to the motion of a surface patch
due to the motion of a surface patch ![]() in
a time
in
a time ![]() is
is
![]() .
The curvature of a sphere is
.
The curvature of a sphere is
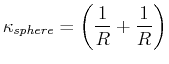 |
(20-4) |
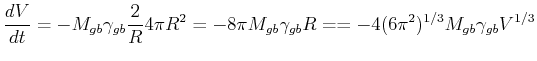 |
(20-5) |
| (20-6) |
| (20-7) |
The problem (and result) is more interesting if the grain doesn't have uniform curvature.

|
|
However, it can still be shown that, even for an irregularly
shaped two-dimensional grain,
![]() const
const![]() .
.