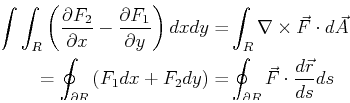Link to Current (updated) notes

Stokes' Theorem

The final generalization of the fundamental theorem of calculus is the relation between a vector function integrated over an oriented surface and another vector function integrated over the closed curve that bounds the surface.

A simplified version of Stokes's theorem has already been discussed--Green's theorem in the plane can be written in full vector form:

$$\begin{split}\int \int_R \left( \ensuremath{\frac{\partial{F_... ...ec{F} \cdot \ensuremath{\frac{d{\vec{r}}}{d{s}}} ds \end{split}$$ (16-7)

as long as the region $R$ lies entirely in the $z=$constant plane.

In fact, Stokes's theorem is the same as the full vector form in Eq. 16-7 with $R$ generalized to an oriented surface embedded in three-dimensional space:

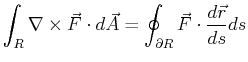$$\int_R \nabla \times \vec{F} \cdot d \vec{A} = \oint_{\partial R} \vec{F} \cdot \ensuremath{\frac{d{\vec{r}}}{d{s}}} ds$$ (16-8)

Plausibility for the theorem can be obtained from Figures 16-1 and 16-2. The curl of the vector field summed over a surface ``spills out'' from the surface by an amount equal to the vector field itself integrated over the boundary of the surface. In other words, if a vector field can be specified everywhere for a fixed surface, then its integral should only depend on some vector function integrated over the boundary of the surface.