Next: Ampere's Law
Up: Lecture_16_web
Previous: Stokes' Theorem
Next: Ampere's Law
Up: Lecture_16_web
Previous: Stokes' Theorem
The divergence theorem and Stokes's theorem are generalizations
of integration that invoke the divergence and curl operations
on vectors.
A familiar vector field is the electromagnetic field and Maxwell's
equations depend on these vector derivatives as well:
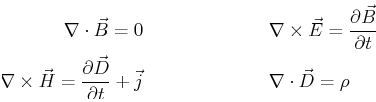 |
(16-9) |
in MKS units and the total electric displacement 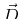 is related
to the total polarization
is related
to the total polarization 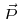 and the electric field
and the electric field 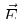 through:
through:
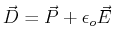 |
(16-10) |
where
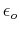 is the dielectric permittivity of vacuum.
The total magnetic induction
is the dielectric permittivity of vacuum.
The total magnetic induction 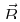 is related to the induced magnetic
field
is related to the induced magnetic
field 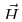 and the material magnetization through
and the material magnetization through
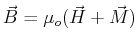 |
(16-11) |
where 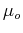 is the magnetic permeability of vacuum.
is the magnetic permeability of vacuum.
© W. Craig Carter 2003-, Massachusetts Institute of Technology