Next: The Divergence Theorem
Up: Lecture_16_web
Previous: Lecture_16_web
Next: The Divergence Theorem
Up: Lecture_16_web
Previous: Lecture_16_web
The fundamental theorem of calculus was generalized in a previous
lecture from an integral over a single variable to an integration
over a region in the plane.
Specifically, for generalizing to Green's theorem in the plane,
a vector derivative of a function integrated over a line
and evaluated at its endpoints was generalized to a vector derivative of a function
integrated over the plane.
Figure 16-1:
Illustrating how Green's theorem
in the plane works.
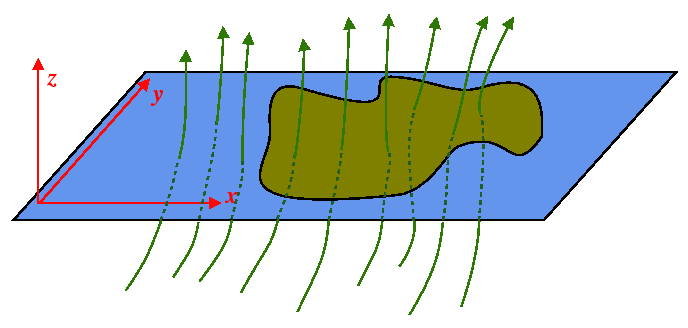
If a known vector function is integrated over a region in the plane
then that integral should only depend on the bounding curve of that
region.

|
Figure:
Illustration of a
generalization to the Green's theorem in the plane:
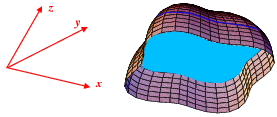
Suppose there is a bowl of a known shape submerged in a fluid with
a trapped bubble.
The bubble is bounded by two different surfaces, the bowl down to
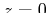 and the planar liquid surface at that height.
Integrating the function
and the planar liquid surface at that height.
Integrating the function
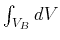 over the bubble gives its
volume.
The volume must also be equal to an integral
over the bubble gives its
volume.
The volume must also be equal to an integral
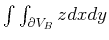 over the (oriented) surface
of the liquid.
However, the volume of bubble can be determined from only the curve
defined by the intersection of the bowl and the planar liquid surface;
so the volume must also be equal to
over the (oriented) surface
of the liquid.
However, the volume of bubble can be determined from only the curve
defined by the intersection of the bowl and the planar liquid surface;
so the volume must also be equal to
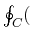 some function
some function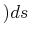 .
.

|
© W. Craig Carter 2003-, Massachusetts Institute of Technology