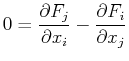Next: Multidimensional Integrals
Up: Lecture_14_web
Previous: Lecture_14_web
Next: Multidimensional Integrals
Up: Lecture_14_web
Previous: Lecture_14_web
Subsections
Consider the type of integral that everyone learns initially:
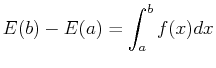 |
(14-1) |
The equation implies that 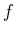 is integrable and
is integrable and
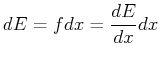 |
(14-2) |
so that the integral can be written in the following way:
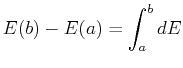 |
(14-3) |
where 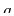 and
and 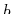 represent ``points'' on some line
where
represent ``points'' on some line
where 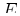 is to be evaluated.
is to be evaluated.
Of course, there is no reason to restrict integration to a
straight line--the generalization is the integration
along a curve (or a path)
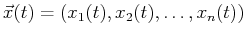 .
.
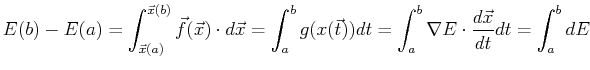 |
(14-4) |
This last set of equations assumes that the gradient exists-i.e., there
is some function  that has the gradient
that has the gradient
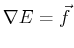 .
.
If the function being integrated along a simply-connected
path (Eq. 14-4)
is a gradient of some scalar
potential, then the path between two integration points
does not need to be specified: the integral is independent of path.
It also follows that for closed paths, the integral of the gradient
of a scalar potential is zero.1
A simply-connected path is one that does not self-intersect or can
be shrunk to a point without leaving its domain.
There are familiar examples from classical thermodynamics of simple
one-component fluids that
satisfy this property:
Where
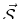 is any other set of variables that sufficiently
describe the equilibrium state of the system (i.e,
is any other set of variables that sufficiently
describe the equilibrium state of the system (i.e, 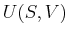 ,
, 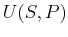 ,
,
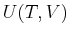 ,
, 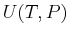 for
for 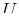 describing a simple one-component fluid).
describing a simple one-component fluid).
The relation
curl grad 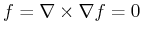 provides method for testing whether some general
provides method for testing whether some general
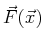 is independent of path. If
is independent of path. If
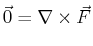 |
(14-7) |
or equivalently,
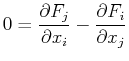 |
(14-8) |
for all variable pairs 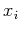 ,
, 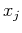 ,
then
,
then
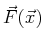 is independent of path.
These are the Maxwell relations of classical thermodynamics.
is independent of path.
These are the Maxwell relations of classical thermodynamics.
MATHEMATICA Example
Example |
| (notebook Lecture-14) |
| (html Lecture-14) |
| (xml+mathml Lecture-14) |
| Path Dependence, Curl, and Curl=0 subspaces
This
example will show that the choice of path matters for
a vector-valued function that does not have vanishing curl
and that it doesn't matter when integrating a function with
vanishing curl.
- Path-dependent/Non-conserving Field
- Verify that the function
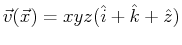 does not have vanishing curl.
does not have vanishing curl.
- Integrate
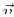 along a path that is wrapped around a cylinder of
radius
along a path that is wrapped around a cylinder of
radius 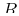 , (e.g.,
, (e.g.,
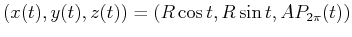 ,
where
,
where
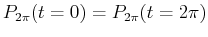 )
)
- Calculate the integral specifically for
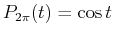 ,
,
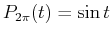 ,
,
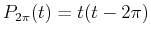 , and
, and
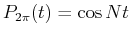 .
.
- Path-independent/Conservative Field
- Verify that, for the function
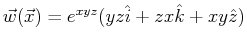 ,
,
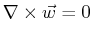 .
In fact,
.
In fact,
 .
.
- Integrate
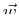 along the same cylindrical-type path as above
and see that the integral always vanishes--it is path-independent.
along the same cylindrical-type path as above
and see that the integral always vanishes--it is path-independent.
- Path independent on a Subspace
- The vector function
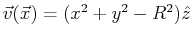 only vanishes on the cylinder or radius
only vanishes on the cylinder or radius 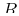 .
.
- It is easy to find
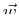 such that
such that
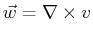 :
:
In fact, because we could add any vector function that has vanishing curl
to 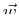 there are an infinite number of
there are an infinite number of 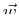 such that
such that
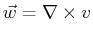 .
.
- Therefore, if we integrate
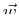 along a path that is restricted to the
cylinder it should be path independent.
along a path that is restricted to the
cylinder it should be path independent.
- Using the same methods as above, we find that the integral on the cylinder will
be independent of
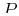 --the vector function
--the vector function 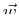 is independent of path
as long as the path remains on the cylinder.
is independent of path
as long as the path remains on the cylinder.
|
© W. Craig Carter 2003-, Massachusetts Institute of Technology
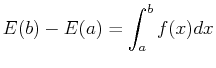
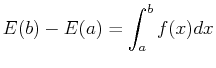
![]() is integrable and
is integrable and
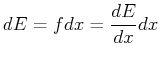
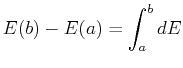
![]() .
.
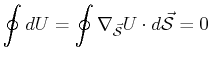
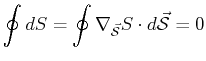
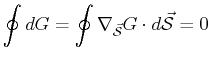
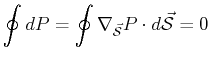
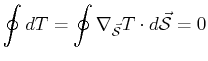
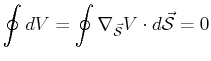
![]() provides method for testing whether some general
provides method for testing whether some general
![]() is independent of path. If
is independent of path. If