Link to Current (updated) notes

Multidimensional Integrals

Perhaps the most straightforward of the higher-dimensional integrations (e.g., vector function along a curve, vector function on a surface) is a scalar function over a domain such as, a rectangular block in two dimensions, or a block in three dimensions. In each case, the integration over a dimension is uncoupled from the others and the problem reduces to pedestrian integration along a coordinate axis.

Sometimes difficulty arises when the domain of integration is not so easily described; in these cases, the limits of integration become functions of another integration variable. While specifying the limits of integration requires a bit of attention, the only thing that makes these cases difficult is that the integrals become tedious and lengthy. MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ removes some of this burden.

A short review of various ways in which a function's variable can appear in an integral follows:

	The Integral	Its Derivative
Function of limits	$$p(x) = \int_{\alpha(x)}^{\beta(x)} f(\xi) d \xi$$	$$\frac{dp}{dx} = f(\beta(x))\frac{d\beta}{dx} - f(\alpha(x))\frac{d\alpha}{dx}$$
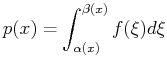
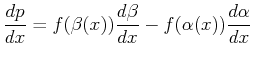
Function of integrand	$$q(x) = \int_{a}^{b} g(\xi, x) d \xi$$	$$\frac{dq}{dx} = \int_{a}^{b} \ensuremath{\frac{\partial{g(\xi, x)}}{\partial{x}}} d \xi$$
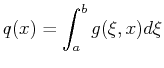
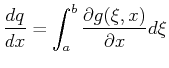
Function of both	$$r(x) = \int_{\alpha(x)}^{\beta(x)} g(\xi,x) d \xi$$	$$\begin{split}\frac{dr}{dx} = f(\beta(x))\frac{d\beta}{dx} - f(\al... ...eta(x)} \ensuremath{\frac{\partial{g(\xi, x)}}{\partial{x}}} d \xi \end{split}$$

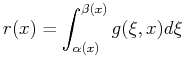
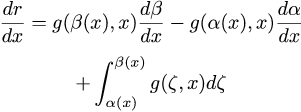
Extra Information and Notes
Potentially interesting but currently unnecessary

Changing of variables is a topic in multivariable calculus that often causes difficulty in classical thermodynamics.

This is an extract of my notes on thermodynamics: http://pruffle.mit.edu/3.00/

Alternative forms of differential relations can be derived by changing variables.

To change variables, a useful scheme using Jacobians can be employed:

$$\begin{split}\ensuremath{\frac{\partial (u , v)}{\partial (x ... ...\ensuremath{\frac{\partial{v(x,y)}}{\partial{x}}}\ \end{split}$$ (14-9)

$$\begin{split}\ensuremath{\frac{\partial (u , v)}{\partial (x ... ...suremath{\frac{\partial (r , s)}{\partial (x , y)}} \end{split}$$ (14-10)

For example, the heat capacity at constant volume is:

$$\begin{split}C_V & = T \ensuremath{ \left( \frac{\partial{S}}... ...left( \frac{\partial{S}}{\partial{P}} \right)_{T} } \end{split}$$ (14-11)

Using the Maxwell relation, $\ensuremath{ \left( \frac{\partial{S}}{\partial{P}} \right)_{T} } = - \ensuremath{ \left( \frac{\partial{V}}{\partial{T}} \right)_{P} }$ ,

$$C_P - C_V = -T \frac{ [ \ensuremath{ \left( \frac{\partial{V}}{\p... ...P} } ]^2 }{ \ensuremath{ \left( \frac{\partial{V}}{\partial{P}} \right)_{T} } }$$ (14-12)

which demonstrates that $C_P > C_V$ because, for any stable substance, the volume is a decreasing function of pressure at constant temperature.

MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-14)

(html Lecture-14)

(xml+mathml Lecture-14)

Potential near a Charged and Shaped Surface Patch Example calculation of the spatially-dependent energy of a unit point charge in the vicinity of a charged planar region having the shape of an equilateral triangle. The energy of a point charge $\vert e\vert$ due to a surface patch on the plane $z=0$ of size $d\xi d\eta$ with surface charge density $\sigma(x,y)$ is:

$$dE(x,y,z,\xi,\eta) = \frac{\vert e\vert \sigma(\xi,\eta) d \xi d \eta}{\vec{r}(x,y,z,\xi,\eta)}$$

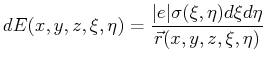
for a patch with uniform charge,

$$dE(x,y,z,\xi,\eta) = \frac{\vert e\vert \sigma d \xi d \eta} {\sqrt{(x - \xi)^2 + (y - \eta)^2 + z^2}}$$

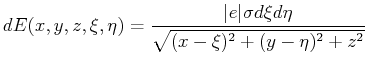
For an equilateral triangle with sides of length one and center at the origin, the vertices can be located at $(0, \sqrt{3}/2)$ and $(\pm{1/2},-\sqrt{3}/6)$ . The integration becomes

$$E(x,y,z) \propto \int_{-\sqrt{3}/6}^{\sqrt{3}/2} \left( \int_{\et... ...2 - \eta} \frac{d\xi} {\sqrt{(x - \xi)^2 + (y - \eta)^2 + z^2}} \right) d \eta$$

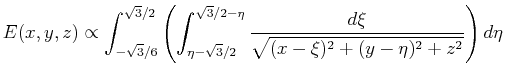
MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ 's syntax is to integrate over the last integration iterator first, and the first iterator last; i.e., the expression:
Integrate[1/r[x,y,z], {x,a,b}, {y,f[x],g[x]}, {z,p[x,y],q[x,y]}]
would integrate over $z$ first, $y$ second, and lastly $x$ . The closed form of the above integral appears to be unknown to MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ . However, the energy can be integrated numerically without difficulty and visualized.