Link to Current (updated) notes

Divergence and Its Interpretation

Coordinate Systems

The above definitions are for a Cartesian $(x,y,z)$ system. Sometimes it is more convenient to work in other (spherical, cylindrical, etc) coordinate systems. In other coordinate systems, the derivative operations $\ensuremath{\nabla}$ , $\ensuremath{\nabla}\cdot$ , and $\ensuremath{\nabla}\times$ have different forms. These other forms can be derived, or looked up in a mathematical handbook, or specified by using the MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ package ``VectorAnalysis.''

MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-13)

(html Lecture-13)

(xml+mathml Lecture-13)

Coordinate System Transformations

The divergence operates on a vector field that is a function of position, $\vec{v}(x,y,z)$ = $\vec{v}(\vec{x})$ = $(v_1 (\vec{x}), v_2(\vec{x}), v_3(\vec{x}))$ , and returns a scalar that is a function of position. The scalar field is often called the divergence field of $\vec{v}$ or simply the divergence of $\vec{v}$ .

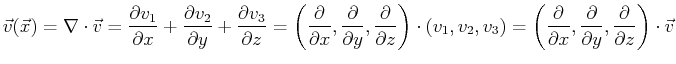$$\vec{v}(\vec{x}) = \ensuremath{\nabla}\cdot \vec{v}= \frac{\parti... ...frac{\partial }{\partial y}, \frac{\partial }{\partial z} \right) \cdot \vec{v}$$ (13-2)

Think about what the divergence means,