The number of different ideas, whether from physical science or other disciplines, that can be understood with reference to the ``meaning'' of a derivative from the calculus of scalar functions is very very large. Our ideas about many topics, such as price elasticity, strain, stability, and optimization, are connected to our understanding of a derivative.
In vector calculus, there are generalizations to the derivative from basic calculus that acts on a scalar and gives another scalar back:
The gradient operation on
![]() ,
,
grad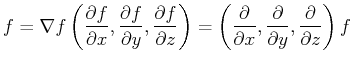 |
(13-1) |
|
MATHEMATICA |
| (notebook Lecture-13) |
| (html Lecture-13) |
| (xml+mathml Lecture-13) |
| Gradient of a several |