The curl is the vector valued derivative of a vector function. As illustrated below, its operation can be geometrically interpreted as the rotation of a field about a point.
For a vector-valued function of ![]() :
:
| (13-3) |
the curl derivative operation is another vector defined by:
curl 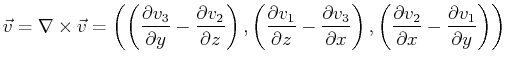 |
(13-4) |
curl 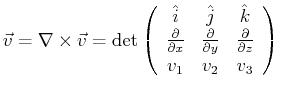 |
(13-5) |
|
MATHEMATICA |
| (notebook Lecture-13) |
| (html Lecture-13) |
| (xml+mathml Lecture-13) |
| Calculating the Curl of a Function
Consider the vector function that is often used in Brakke's
Surface Evolver program:
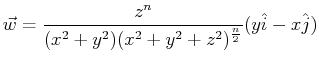
This can be shown easily, using MATHEMATICA
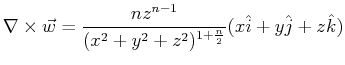
which is spherically symmetric for
|
One important result that has physical implications is
that a the curl of a gradient is always zero:
![]() :
:
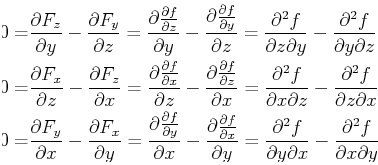 |
(13-7) |
Another interpretation is that gradient fields are curl free, irrotational, or conservative.
The notion of conservative means that, if a vector function can be derived as the gradient of a scalar potential, then integrals of the vector function over any path is zero for a closed curve--meaning that there is no change in ``state;'' energy is a common state function.
Here is a picture that helps visualize why the curl invokes names associated with spinning, rotation, etc.
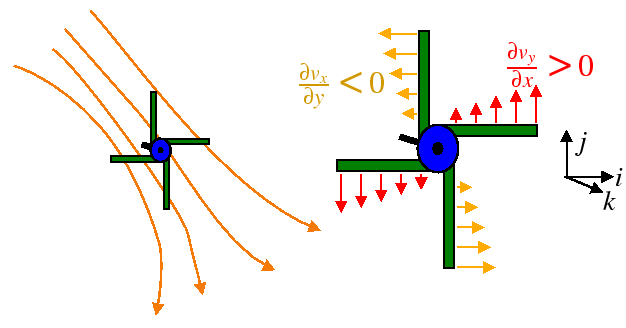
|
|
Another important result is that divergence of any curl is
also zero, for
![]() :
: