Link to Current (updated) notes

Scalar Functions with Vector Argument

In materials science and engineering, the concept of a spatially varying function arises frequently:

For example:

Concentration

$c_i(x,y,z) = c_i(\vec{x})$ is the number (or moles) of chemical species of type $i$ per unit volume located at the point $\vec{x}$ .

Density

$\rho(x,y,z) = \rho(\vec{x})$ mass per unit volume located at the point $\vec{x}$ . a point $\rho(x,y,z) = \rho(\vec{x})$ .

Energy Density

$u(x,y,z) = u(\vec{x})$ energy per unit volume located at the point $\vec{x}$ .

The examples above are spatially dependent densities of ``extensive quantities.''

There are also spatially variable intensive quantities:

Temperature

$T(x,y,z) = T(\vec{x})$ is the temperature which would be measured at the point $\vec{x}$ .

Pressure

$P(x,y,z) = P(\vec{x})$ is the pressure which would be measured at the point $\vec{x}$ .

Chemical Potential

$\mu_i(x,y,z) = \mu_i(\vec{x})$ is the chemical potential of the species $i$ which would be measured at the point $\vec{x}$ .

Each example is a scalar function of space--that is, the function associates a scalar with each point in space.

A topographical map is a familiar example of a graphical illustration of a scalar function (altitude) as a function of location (latitude and longitude).

How Confusion Can Develop in Thermodynamics

However, there are many other types of scalar functions of several arguments, such as the state function: $U = U(S,V,N_i)$ or $P = P(V,T,N_i)$ . It is sometimes useful to think of these types of functions a scalar functions of a ``point'' in a thermodynamics space.

However, this is often a source of confusion: notice that the internal energy is used in two different contexts above. One context is the value of the energy, say 128.2 Joules. The other context is the function $U(S,V,N_i)$ . While the two symbols are identical, their meanings are quite different.

The root of the confusion lurks in the question, ``What are the variables of $U$ ?'' Suppose that there is only one (independent) chemical species, then $U(\cdot)$ has three variables, such as $U(S,V,N)$ . ``But what if $S(T,P,\mu)$ , $V(T,P,\mu)$ , and $N(T,P,\mu)$ are known functions, what are the variables of $U$ ?'' The answer is, they are any three independent variables, one could write $U(T,P,\mu) = U(S(T,P,\mu),V(T,P,\mu),N(T,P,\mu))$ and there are six other natural choices.

The trouble arises when variations of a function like $U$ are queried--then the variables that are varying must be specified.

For this reason, it is either a good idea to keep the functional form explicit in thermodynamics, i.e.,

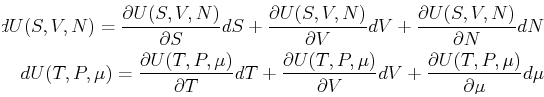$$\begin{split}dU(S,V,N) = \ensuremath{\frac{\partial{U(S,V,N)}... ...{\frac{\partial{U(T,P,\mu)}}{\partial{\mu}}} d\mu\ \end{split}$$ (12-6)

or use, the common thermodynamic notation,

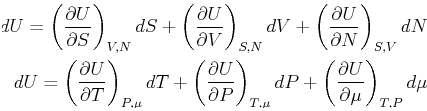$$\begin{split}dU = \ensuremath{ \left( \frac{\partial{U}}{\par... ...{\partial{U}}{\partial{\mu}} \right)_{T,P} } d\mu\ \end{split}$$ (12-7)