Link to Current (updated) notes

Polar Form of Complex Numbers

There are physical situations in which a transformation from Cartesian ($x, y$ ) coordinates to polar (or cylindrical) coordinates ($r, \theta$ ) simplifies the algebra that is used to describe the physical problem.

An equivalent coordinate transformation for complex numbers, $z = x + \imath y$ , has an analogous simplifying effect for multiplicative operations on complex numbers. It has been demonstrated how the complex conjugate, $\bar{z}$ , is related to a reflection--multiplication is related to a counter-clockwise rotation in the complex plane. Counter-clockwise rotation corresponds to increasing $\theta$ .

The transformations are:

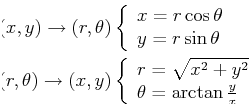$$\begin{split}(x,y) \rightarrow (r, \theta) & \left\{ \begin{a... ... \theta = \arctan \frac{y}{x}\ \end{array} \right. \end{split}$$ (08-4)

where $\arctan \in (-\pi,\pi]$ .

Multiplication, Division, and Roots in Polar Form

One advantage of the polar complex form is the simplicity of multiplication operations:

DeMoivre's formula:

$$z^n = r^n (\cos n \theta + \imath \sin n \theta)$$ (08-5)

$$\sqrt[n]{z} = \sqrt[n]{z} (\cos \frac{\theta + 2 k \pi}{n} + \imath \sin \frac{\theta + 2 k \pi}{n})$$ (08-6)

MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-07)

(html Lecture-07)

(xml+mathml Lecture-07)

Polar Form of Complex Numbers