Link to Current (updated) notes

Exponentiation and Relations to Trignometric Functions

Exponentiation of a complex number is defined by:

$$e^z = e^{x + iy} = e^x (\cos y + \imath \sin y)$$ (08-7)

Exponentiation of a purely imaginary number advances the angle by rotation:

$$e^{\imath y} = \cos{y} + \imath \sin{y}$$ (08-8)

combining Eq. 8-8 with Eq. 8-7 gives the particularly useful form:

$$z = x + \imath y = r e^{\imath \theta}$$ (08-9)

and the useful relations (that can be obtained simply by considering the geometry of the complex plane)

$$\begin{array}{lllll} e^{2 \pi \imath} = 1 & e^{\pi \imath} = ... ...ath} = \imath & e^{-\frac{\pi}{2} \imath} = -\imath \end{array}$$ (08-10)

Judicious subtraction of powers in Eq. 8-8 and generalization gives the following useful relations for trigonometric functions:

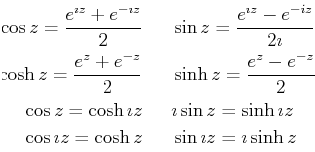$$\begin{split}\cos z = \frac{e^{\imath z} + e^{-\imath z}}{2} ... ... z \hspace{0.25in} & \sin \imath z = \imath \sinh z \end{split}$$ (08-11)

MATHEMATICA$^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-07)

(html Lecture-07)

(xml+mathml Lecture-07)

Numerical precision and rounding of complex numbers
Roots of polynomial equations