
 Next: Polar Form of Complex Numbers
Up: Lecture_08_web
Previous: Lecture_08_web
Next: Polar Form of Complex Numbers
Up: Lecture_08_web
Previous: Lecture_08_web
Subsections
With
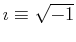 , the complex numbers can be
defined as the space of numbers spanned by the vectors:
, the complex numbers can be
defined as the space of numbers spanned by the vectors:
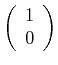 and and 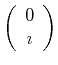 |
(08-1) |
so that any complex number can be written as
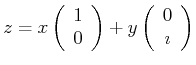 |
(08-2) |
or just simply as
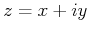 |
(08-3) |
where 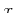 and
and 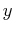 are real numbers.
Re
are real numbers.
Re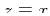 and
Im
and
Im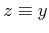 .
.
Complex Plane and Complex Conjugates
Because the complex basis can be written in terms of the
vectors in Equation 8-1, it is natural
to plot complex numbers in two dimensions--typically these
two dimensions are the ``complex plane'' with
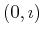 associated
with the
associated
with the 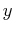 -axis and
-axis and 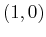 associated with the
associated with the 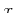 -axis.
-axis.
The reflection of a complex number across the real axis is
a useful operation.
The image of a reflection across the real axis has some
useful qualities and is given a special name--``the complex
conjugate.''
Figure:
Plotting the complex number 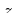 in the
complex plane:
The complex conjugate (
in the
complex plane:
The complex conjugate (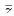 ) is a reflection across the real
axis; the minus (
) is a reflection across the real
axis; the minus (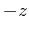 ) operation is an inversion through
the origin; therefore
) operation is an inversion through
the origin; therefore
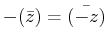 is equivalent
to either a reflection across the imaginary axis or an inversion
followed by a reflection across the real axis.
is equivalent
to either a reflection across the imaginary axis or an inversion
followed by a reflection across the real axis.
The real part of a complex number is the projection of
the displacement in the real
direction and also the average of the complex number and
its conjugate:
Re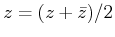 .
The imaginary part is the displacement projected onto the imaginary
axis, or the complex average of the complex number and
its reflection across the imaginary axis:
Im
.
The imaginary part is the displacement projected onto the imaginary
axis, or the complex average of the complex number and
its reflection across the imaginary axis:
Im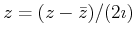 .
.

|
© W. Craig Carter 2003-, Massachusetts Institute of Technology
![]() , the complex numbers can be
defined as the space of numbers spanned by the vectors:
, the complex numbers can be
defined as the space of numbers spanned by the vectors:
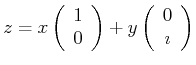
![]() associated
with the
associated
with the ![]() -axis and
-axis and ![]() associated with the
associated with the ![]() -axis.
-axis.
