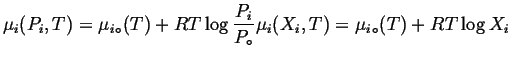 |
(20-13) |
In an ``ideal solution,'' the system is made slightly more complicated by allowing chemical potential to become a function of pressure.
| (20-14) |
In the general case, a new term (the activity ![]() ) is introduced to generalize the
dependence on concentration:
) is introduced to generalize the
dependence on concentration:
| (20-15) |
![]() is called the ``activity of species
is called the ``activity of species
![]() ''--it is a ``generalized composition.''
Factoring out the
''--it is a ``generalized composition.''
Factoring out the ![]() :
:
| (20-16) |
![]() is called an activity coefficient.
In the most general case, it
could also be a function of
is called an activity coefficient.
In the most general case, it
could also be a function of ![]() , but limiting cases
where it is independent of
, but limiting cases
where it is independent of ![]() will be discussed later.
will be discussed later.