- ... system.1
- For the partial derivative with
respect to
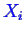 in Equation 20-3, there is a constraint between
the variables
in Equation 20-3, there is a constraint between
the variables
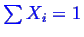 , that must be considered when taking
the derivative of the molar free energy.
Later, we will derive an important graphical construction for the determination
of
, that must be considered when taking
the derivative of the molar free energy.
Later, we will derive an important graphical construction for the determination
of
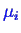 from curves of
from curves of
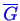 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mixture2
- That is a system of particles that
occupy a neglible volume and are non-interacting.
Each particle is identified with a chemical species.
If the species are assumed to react, then the combinations of
particles to form another vary according to the stoicheometric
coefficients of a chemical reaction of
the form

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline3301#�3
- All the
chemical species
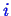 should use the same reference pressure so the
subscript can be dropped.
Whenever a subscript appears below, it will refer to a partial pressure, i.e.,
should use the same reference pressure so the
subscript can be dropped.
Whenever a subscript appears below, it will refer to a partial pressure, i.e.,
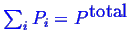
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gas.4
- An ideal single gas:
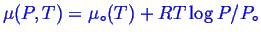 . Note, you will often see formulae like
. Note, you will often see formulae like
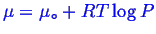 , you know that
, you know that
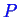 cannot
have units-so a convenient
cannot
have units-so a convenient
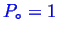 has been
picked.
has been
picked.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.