The Chemical Potential in a Closed System

It was demonstrated that a system that can exchange energy and volume with a reservoir is in equilibrium with the reservoir when the pressure is the same in the system as in the reservoir. This idea can be extended to a complicated set of many interacting subsystems to arrive at the conclusion that pressure and temperature must be uniform at equilibrium.

Recall the method that was used to demonstrate the uniformity of $P$ and $T$: from a conservation principle (i.e., constant internal energy and constant volume) for an extensive variable, and with a maximal principle for entropy (i.e., $\ensuremath{{dS}_{\mbox{universe}}} = 0$) it followed that the intensive variables associated with the conserved quantities must be equal at equilibrium.

At constant temperature and pressure, the Gibbs free energy of the system is minimized at equilibrium-this is another extremal principle With another conservation principle, another equality can be derived. For a closed system, the total number or atoms or molecules of a particular type is conserved; this is an additional constraint for each species in the $f$ possible phases:

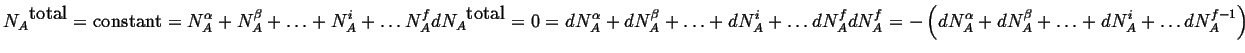$$\input{equations/closed-conserved}$$ (20-1)

where the equations are written out for the $A$-type atoms.

Using a similar expression for each of the $C$-conserved species and putting this into the expression for $dG$:

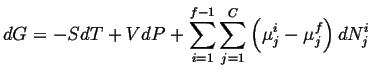$$\input{equations/dG-conserved}$$ (20-2)

Because $G$ is minimized at equilibrium at constant $P$ and $T$, it follows that if any species $j$ can be exchanged between the $i$-phase and the $f$-phase (i.e., one can consider virtual changes with nonzero values of $dN_i^j = - dN_i^f$) then it follows from Equation 20-2 that $\mu_j^i = \mu_j^f$ at equilibrium.

To see this consider three different cases:

$\mu_j^i > \mu_j^f$

Species can flow from the $i$-phase into the $f$-phase ( $dN_i^j < 0$) and the Gibbs free energy can be decreased at constant $P$ and $T$ ( $(dG)_{P,T} < 0$).

$\mu_j^i < \mu_j^f$

Species can flow from the $f$-phase into the $i$-phase ( $dN_i^j > 0$) and the Gibbs free energy can be decreased at constant $P$ and $T$ ( $(dG)_{P,T} < 0$).

$\mu_j^i = \mu_j^f$

Any direction of flow of species ( $dN_i^j \geq 0$ or $dN_i^j < 0$) will not decrease $G$ ( $(dG)_{P,T} = 0$).

In other words, a chemical species could be spontaneously transported from a phase of larger chemical potential to one of lower chemical potential.

At equilibrium, the chemical potential of any transportable species,

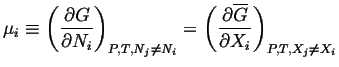$$\input{equations/mu-forms}$$ (20-3)

must be uniform throughout the system.¹