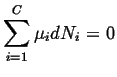 |
(20-4) |
We begin by applying the condition that applies for equilibrium to a a single phase mixture of ideal gases at constant pressure and temperature.
To apply equilibrium condition:
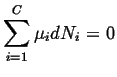 |
(20-4) |
to an ideal gas, an expression for the Gibbs free energy
associated with each component is calculated.
For an ideal gas,
![]() is a function of
is a function of
![]() only. And since
only. And since
![]() ,
,
![]() is a function of
is a function of
![]() only.
only.
![]() is the Gibbs free energy per
mole of species
is the Gibbs free energy per
mole of species
![]() (this will be shown to be true later),
so we need to find an expression for:
(this will be shown to be true later),
so we need to find an expression for:
| (20-5) |
To find a model for the chemical potential in an
ideal gas mixture2,
one might imagine that the system is in contact
with
![]() pistons and each of the pistons only interacts with one gas.
The total pressure is the sum of the partial pressures on each of the pistons.
Or, one might associate a sub-volume
pistons and each of the pistons only interacts with one gas.
The total pressure is the sum of the partial pressures on each of the pistons.
Or, one might associate a sub-volume
![]() with each of the
with each of the
![]() components.
components.
For an ideal gas,
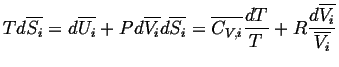 |
(20-6) |
Because the individual volumes associated with each gas species
are the ``internal degrees of freedom'' which
may adjust themselves so that the system attains equilibrium,
an expression for the
the molar entropy can be calculated for any ideal gas species occupying
volume
![]() at some temperature
at some temperature
![]() by
integrating that volume from some reference state.
by
integrating that volume from some reference state.
It will be useful to introduce a particular reference state,
![]() , which is the volume that a mole of isolated gas
would occupy at some
temperature
, which is the volume that a mole of isolated gas
would occupy at some
temperature
![]() and some reference pressure
and some reference pressure
![]() 3
3
Therefore changing the state of each of species
![]() from its reference
state to any molar volume
from its reference
state to any molar volume
![]() at constant temperature
can be calculated by integrating Equation 20-6
along an isotherm:
at constant temperature
can be calculated by integrating Equation 20-6
along an isotherm:
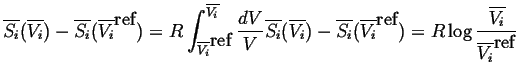 |
(20-7) |
And because
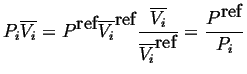 |
(20-8) |
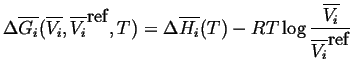 |
(20-9) |
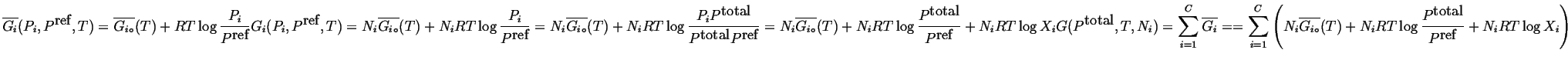 |
(20-10) |
if we take
![]() to be some
convenient standard state (i.e. STP)
then
to be some
convenient standard state (i.e. STP)
then
![]() is the
partial pressure of the gaseous species
is the
partial pressure of the gaseous species
![]() with respect to one atmosphere.
with respect to one atmosphere.
![]() is the numerical value of the partial pressure
of the
i
is the numerical value of the partial pressure
of the
i![]() species, but it is really unitless.
species, but it is really unitless.
Typically, a standard is adopted where all pressure measurements
are assumed to be in atmospheres and thus the
![]() term
is written as
term
is written as
![]() where it is understood that
where it is understood that
![]() is exactly the
numerical value of
the unitless
is exactly the
numerical value of
the unitless
![]() and there is no difficulty in carrying around
units like log(atmospheres).
We will adopt this standard below.
and there is no difficulty in carrying around
units like log(atmospheres).
We will adopt this standard below.
From these considerations derives an expression for the chemical potentials of ideal gases in a mixture:
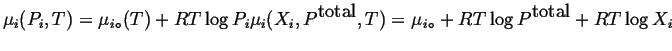 |
(20-11) |
Compare this to
![]()
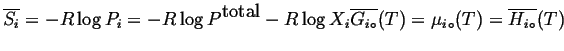 |
(20-12) |
for an ideal gas mixture.