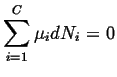Equilibrium Compositions in an Ideal Reacting Gas Mixture

The simple expression for the chemical potentials in an ideal gas can be put into the equilibrium condition:

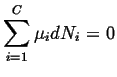$$\input{equations/gd}$$ (20-17)

and equilibrium amounts of material can be calculated.

If we have a closed system (fixed number of moles of the independent species), then

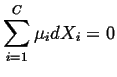$$\input{equations/mgd}$$ (20-18)

A Simple Example

Consider the gaseous reaction

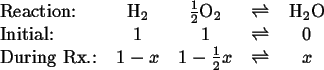
Therefore, $dX_{\mbox{H}_{2}} = -dX_{\ensuremath{\mbox{H}_2\mbox{O}}}$ and $dX_{\mbox{O}_{2}} = - \frac{1}{2} dX_{\ensuremath{\mbox{H}_2\mbox{O}}}$ (Every mole of hydrogen gas that appears is associated with the disappearance of one mole of water vapor; every mole of water vapar that appears is associated with the disappearance of one half a mole of oxygen gas).

Therefore, the condition for equilibrium (Equation 20-18) for an ideal gas mixture becomes:

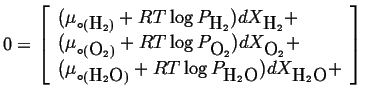$$\input{equations/mu-equil}$$ (20-19)

which is possible only if

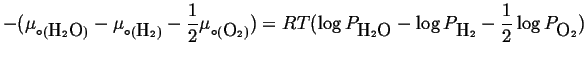$$\input{equations/14-6A}$$ (20-20)

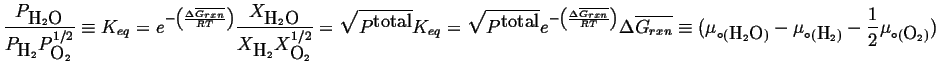$$\input{equations/14-6B}$$ (20-21)

In general for ideal gas mixture with reaction

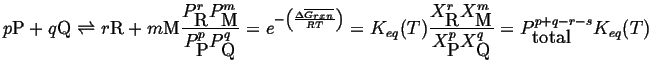$$\input{equations/gen-rx-eq}$$ (20-22)

where the molar free energy change of the reaction is:

and generalizing even more

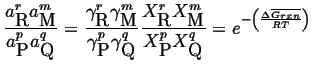$$\input{equations/gen-gen-rx-eq}$$ (20-23)