A Slightly More Complicated Worked Example

Let's consider a more complicated gaseous reaction:

$$\input{equations/co2-h2o}$$ (20-24)

Suppose we have a container at 1 atm and at 1000 ${}^\circ$C with initially two moles of water vapor and one mole of carbon dioxide.

Here are some questions that one might ask:

How many moles of oxygen gas will exist at equilibrium?

If the reaction is carried out at a different pressure, how will the concentration of carbon monoxide vary?

The first question may seem a little odd--there appears to be no oxygen in the reaction 20-24.

However, if reaction 20-24 is written as the sum of two reactions:

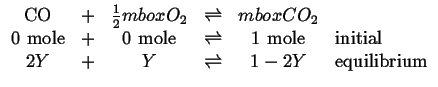$$\input{equations/co2-o2}$$ (20-25)

and

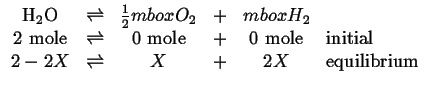$$\input{equations/h2-o2}$$ (20-26)

Then it is clear that oxygen plays a role in the reaction 20-24 as the there are two independent reactions contained in the three reactions 20-24, 20-25. and 20-26.

Furthermore, the sum of the standard free energies for the reaction will also add like the reactions and each of the reactions will have a standard reaction and the dependent reaction will be related to the others:

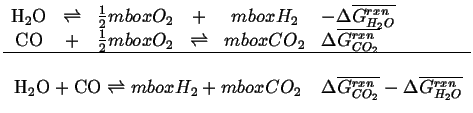$$\input{equations/combined-co2-h2o}$$ (20-27)

The total number of moles of ideal gas in the system at equilibrium will be $\ensuremath{{N}^{\mbox{total}}} = 3 + X + Y$. (n.b., the reaction 20-25 produces $Y$ moles and the reaction 20-26 prooduces $X$ moles in addition to the initial 3 moles.) Every independent reaction must be at equilibrium independently Therefore we can write the two equilibrium conditions for the reaction 20-25

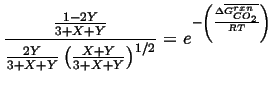$$\input{equations/co2-o2-eq}$$ (20-28)

and for reaction 20-26,

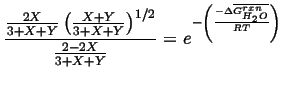$$\input{equations/h2-o2-eq}$$ (20-29)

so there are two independent equations and two unknowns, so it is now algebra to find $X$ and $Y$ and therefore the concentration of oxygen $(X + Y)/(3 + X + Y)$.

To find how the concentration of carbon monoxide depends on pressure, rewrite Eq. 20-28 in terms of partial pressures:

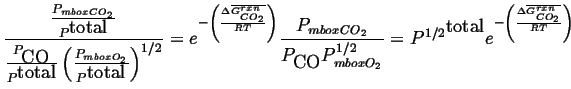$$\input{equations/co2-o2-eq-pp}$$ (20-30)