 |
Last Time
Growth of Precipitates (After Nucleation
Coarsening
Coarsening: Mean Field Theories and Particle Size Distributions
Gibbs-Thompson Effect
Grain Growth
Continuous Transformations--Introduction
In previous lectures on morphological evolution by surface diffusion, interface motion arises even though there is no transportation of material through the interface.
For the case of evaporation-condensation, interface motion arises because material is transforming from a state on one side of the interface into the state on the other side of the interface.
Evaporation-condensation is a simple example of a kinetic process associated with a phase transformation: interface velocity is related to the rate (volume/time) of phase transformation per unit area of interface. Discussions of phase transformations are facilitated with a definition of phase The concept of a phase is often confused with heterogeneity. It will become apparent that a system with multiple phases is necessarily heterogeneous and necessarily has interfaces However, the converse--a heterogeneous system with interfaces necessarily has multiple phases--is not true and is easily proved by the existence of polycrystalline single phase material or that of antiphase boundaries.
A homogeneous part of a system that can be identified as ``physically different'' from another part of the system. Physically different implies that the two homogeneous subsystems are not related by a combined rotation and translation. A phase is always separated from another phase by an identifiable interface.
Pedestrian examples are the solid phases, liquid phase, and vapor phase of pure water where the homogeneous phase can be identified by homogeneous values of the mass density or enthalpy density--the interface can be identified by those regions where the field parameters representing densities of equilibrium extensive quantities are spatially variable. Less obvious examples are the FCC and BCC phases of iron-carbon-nickel-chromium steel or the ferromagnetic and non-ferromagnetic phases of LaSrMnO manganites.
I'll take this opportunity to quote one of my heros:
We may call such bodies as differ in composition or state, different phases of the matter considered, regarding all bodies which differ only in quantity and form as different examples of the same phase.
&dotfill#dotfill;J. W. GIBBS in Trans. Connecticut Acad. III. (1875) page 152
 |
The motion of a grain boundary or an antiphase domain boundary does not transform material as it passes through it. The material is re-ordered but not transformed. Nevertheless, it is useful to introduce a field parameter characterizing the local symmetry or spatial orientation of a material. Such a field parameter would have the characteristic of being uniform except in the vicinity of grain boundary or antiphase domain boundary.
In either case, the kinetic evolution of the relevant field parameter becomes a convenient means to track the motion of the interface because the interface can be co-located at values of the field parameter intermediate to its homogeneous values in the abutting material.
Such field parameters are generically called order parameters. Although it may be that ``order parameter'' has a natural conceptual association to the case of geometrical variants of a single phase, it is consistent with the use of order parameters in the Landau expansion of a free energy density about its equilibrium density. We shall use order parameters in either case.
The hypothesis that an order parameter changes continously through an interface is connected to questions of whether a phase change or geometrical change can be continuous transformations. In other words, a phase or geometrical variant can be generated within another by a continuous process.
The process of the formation of a new phase from an existing phase can be classified into two categories: continuous and discontinuous phase transitions.
Discontinuous phase transitions occur by nucleation--a process that Gibbs called, ``... initially small in extent but great in degree.''1
Degree refers to quantity that characterized a phase and extent refers a length scale. Nucleation will be treated in subsequent lectures.
Continuous phase transitions can be treated with the evolution of continuous order parameter fields--processes that Gibbs called, ``initially is small in degree, but may be great in its extent in space.''
Considerations of the development of a continuous phase transformations or geometrical transform should begin with a careful examination of order parameters.
Order Parameters
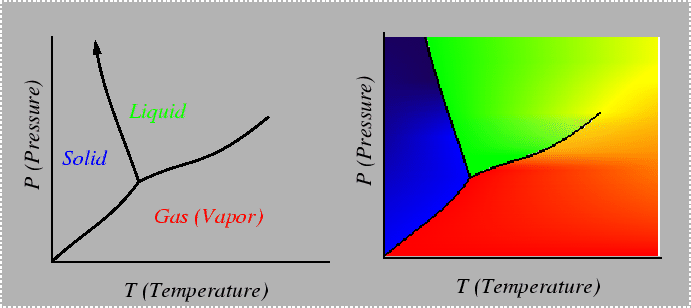
Consider a system in which composition cannot be varied, such as a pure material. The Gibbs phase rule indicates that there is only one degree of freedom in a system that can characterized by temperature and pressure only. One degree of freedom implies that for conditions in which two phases are in equilibrium, there must be a relation between temperature and pressure. Such a relation can be derived by considering the Gibbs-Duhem relationship in each of the phases--for example, if the two phases are solid and liquid:
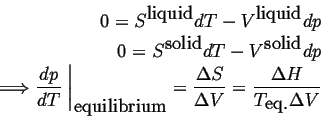 |
(22-1) |
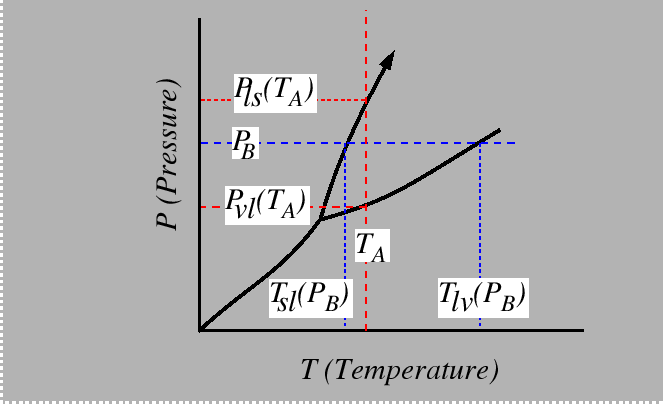
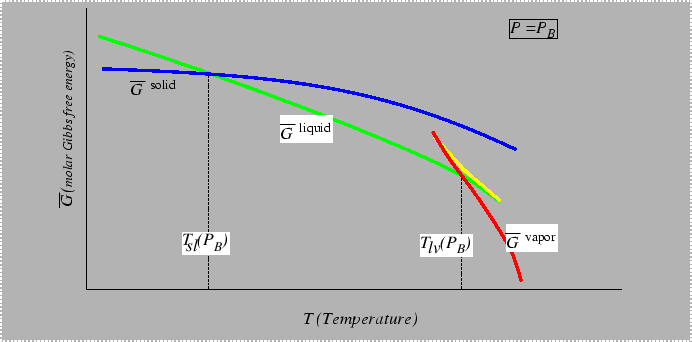
Consider the behavior of the molar free energy (or
![]() ) on slices of Figure 22-1
at constant
) on slices of Figure 22-1
at constant ![]() and
and ![]() :
:
 |
 |
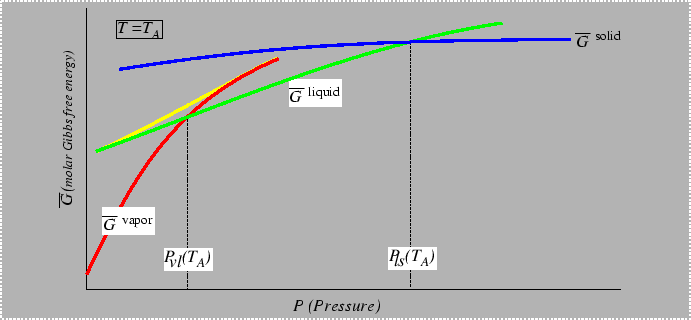 |
What would the plot look like with two extensive variables plotted?
The example in 22-5 is reminiscent of a phase diagram with a miscibility gap:
 |
In fact, if one of the chemical potentials that can be derived by the graphical tangent intercept method was plotted as a function of composition, it would look very similar to the "spiny-looking" curves in Figs 22-3 and 22-3.
In the case of a phase transformation, the equilibrium values of
the density of an extensive quantity,
such as the concentration or composition
![]() ,
can be used as an order parameter.
For geometric transformations or order-disorder, a similar approach
of equilibrium hidden variables is implicit in a Landau expansion.2.
,
can be used as an order parameter.
For geometric transformations or order-disorder, a similar approach
of equilibrium hidden variables is implicit in a Landau expansion.2.
Consider two phases that differ by an order parameter ![]() that could
be associated with the displacement of an atom away from a crystalline
inversion center, such as in a piezoelectric transition.
The equilibrium state of the crystal as an arbitrary function of
a fixed temperature and pressure can be approximated as a series in
the terms
that could
be associated with the displacement of an atom away from a crystalline
inversion center, such as in a piezoelectric transition.
The equilibrium state of the crystal as an arbitrary function of
a fixed temperature and pressure can be approximated as a series in
the terms ![]() ,
, ![]() , and
, and ![]() :
:
| (22-2) |
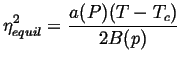 |
(22-3) |
In the case of phase transformations above, the molar
volume could be used as a local indicator of which phase is
present--
![]() can be used as an order parameter
field.
Similarly,
spatial variations of a field
can be used as an order parameter
field.
Similarly,
spatial variations of a field
![]() could be used as an order
parameter to indicate whether a phase is in its centrosymmetric or
a piezoelectric phase--and positions where
could be used as an order
parameter to indicate whether a phase is in its centrosymmetric or
a piezoelectric phase--and positions where
![]() is large
would identify interfaces.
is large
would identify interfaces.
Because a common description language can be developed, it is useful to consider the similarities between different kinds of order parameters; i.e, the densities of extensive quantities that are used as order parameters for phase transformations and the geometrical (or hidden) variables that serve as order parameters that can be used to identify an interface in a single phase material. However, differences between the two types of order parameters will have important consequences on the kinetics of their evolution.
An important distinction is that one order parameter (e.g.,
![]() )
is locally conserved--local changes can only arise from
a flux divergence in the absence of sources and sinks.
The other type of order parameter is not locally conserve; e.g.,
a measure of disorder
)
is locally conserved--local changes can only arise from
a flux divergence in the absence of sources and sinks.
The other type of order parameter is not locally conserve; e.g.,
a measure of disorder
![]() can change with no
associated flux.
can change with no
associated flux.
The ordering reaction does not require long-range diffusion, but the decomposition reaction must move mass over long distances.
In the appendix to these notes, it is demonstrated how the changes in free energy depend on whether flux is required or not. The important results can be summarized as follows:
Therefore, an order parameter can always decrease the free energy
by picking a variation
![]() with a sign that makes the product in
Eq. 22-23 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
with a sign that makes the product in
Eq. 22-23 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
In fact, it can be shown that the sign of the diffusivity, ![]() , for
concentration flux is given by the second derivative
, for
concentration flux is given by the second derivative
![]() .
This has the effect of causing ``up-hill'' diffusion.
.
This has the effect of causing ``up-hill'' diffusion.
Kinetics and Diffuse Interfaces
If transformations occur without nucleation, then the thermodynamics must account for continuous variations of thermodynamic state variables. These continuous variations are called ``diffuse interfaces'' and they are addressed in this section. The important result is that the local free energy density has a contribution due to gradients of thermodynamic state variables.
The theory for the free energy of inhomogeneous systems was developed by
Cahn and Hilliard in 1958.
The theory was originally developed to account for contributions to
the free energy from gradients in the composition--or any other
conserved field.
The diffuse interface method was extended to non-conserved order parameters
by Allen and Cahn (1979) in their study of the kinetics of
the order-disorder transition.
The theories for both can be developed in parallel since their construction
follows from the same principles.
![]() describes any conserved field quantity
(like the concentration field in a closed system) and
describes any conserved field quantity
(like the concentration field in a closed system) and
![]() represents any non-conserved order parameter field.
represents any non-conserved order parameter field.
A two-phase system with a miscibility gap at equilibrium with a
planar interface will have an
equilibrium composition profile ![]() through the interfacial region.
The form of the equilibrium composition distribution is determined
by the
through the interfacial region.
The form of the equilibrium composition distribution is determined
by the ![]() which minimizes
which minimizes ![]() ,
the total free energy of the system.
Similarly, a system that tends to form long-range ordered domains will
have a distribution of order,
,
the total free energy of the system.
Similarly, a system that tends to form long-range ordered domains will
have a distribution of order, ![]() , across a
planar interface between two identical domains having
different local minima in their order parameters.
, across a
planar interface between two identical domains having
different local minima in their order parameters.
Example profiles, ![]() and
and ![]() , through diffuse interfaces
in these two types of systems
are shown schematically below:
, through diffuse interfaces
in these two types of systems
are shown schematically below:
The profiles ![]() and
and ![]() are continuous and
the compositions
are continuous and
the compositions
![]() and
and
![]() are the
equilibrium compositions of the bulk phases.
The values of order parameter
are the
equilibrium compositions of the bulk phases.
The values of order parameter ![]() and
and ![]() correspond to
local minima in the free energy.
correspond to
local minima in the free energy.
Let ![]() stand for either
stand for either ![]() or
or ![]() .
Also, let
.
Also, let
![]() be the free energy of a small volume
be the free energy of a small volume ![]() which has average composition
which has average composition ![]() and a gradient
and a gradient ![]() across it.
If the free energy density is expanded about its homogeneous value
across it.
If the free energy density is expanded about its homogeneous value
![]() (presumably a known function) then
then
(presumably a known function) then
then
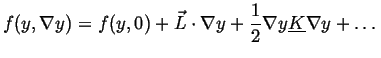 |
(22-6) |
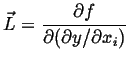 |
(22-7) |
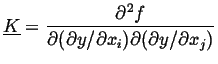 |
(22-8) |
If homogeneous material has a center of symmetry, the free energy
cannot depend on the direction of the gradient and thus
![]() and
and
![]() will be a symmetric matrix.
Furthermore, if the homogeneous material is isotropic (or cubic),
then
will be a symmetric matrix.
Furthermore, if the homogeneous material is isotropic (or cubic),
then
![]() will be a diagonal matrix (with components
will be a diagonal matrix (with components ![]() along the
diagonal), then
free energy density is, to second order:
along the
diagonal), then
free energy density is, to second order:
Only the second term
contributes to the free energy only in the region near the interface
(where the gradient is non-zero).
The gradient-energy coefficient ![]() is a parameter which
contributes to the interfacial area. However, it is not the
only term which contributes: as the composition profile
traverses the interface region,
compositions from the non-equilibrium parts of the free energy curve
are contributing to the excess free energy
associated with the interface as well.
is a parameter which
contributes to the interfacial area. However, it is not the
only term which contributes: as the composition profile
traverses the interface region,
compositions from the non-equilibrium parts of the free energy curve
are contributing to the excess free energy
associated with the interface as well.
It is possible to calculate equilibrium profiles in terms of the
parameters in Eq. 22-9.
However, our purpose is describe the kinetics of how
an arbitrary distribution
![]() evolves towards equilibrium.
evolves towards equilibrium.
We will take a variational calculus approach. The treatment below assumes no prior knowledge of the calculus of variations and will serve as an introduction to the subject.
The total free energy of the entire system (occupying the domain ![]() ) is:
) is:
If the field
![]() is changing with
velocity
is changing with
velocity
![]() , the is the rate of change of
, the is the rate of change of ![]() is
is
![$\displaystyle \frac{\partial F}{\partial t} \ensuremath{\left.\mbox{\rule{0pt}{16pt}}\right\vert}_{t=0} = \int_\Omega [ f'(y) v + K \nabla y \cdot \nabla v ] dV$](img67.gif) |
(22-12) |
using
| (22-13) |
The boundary integral vanishes if
![]() , which
would be the case if
, which
would be the case if
![]() had fixed boundary
values4;
or, if the projections of the gradients onto the boundary vanish.
If these two cases are not satisfied,
then when the volume to surface ratio is greater than
the inherent diffusion length,
the system may be considered to be large enough so that
the contributions due
to boundary can be neglected.
had fixed boundary
values4;
or, if the projections of the gradients onto the boundary vanish.
If these two cases are not satisfied,
then when the volume to surface ratio is greater than
the inherent diffusion length,
the system may be considered to be large enough so that
the contributions due
to boundary can be neglected.
The change in total energy in Eq. 22-14 is the sum of local
variations:
![]() .
Therefore, the largest possible increase of
.
Therefore, the largest possible increase of ![]() is when the flow,
is when the flow,
![]() , is proportional to
, is proportional to
Therefore,
Equation 22-15 is the functional gradient of ![]() .5Sometimes Eq. 22-15 is called the variational derivative
of
.5Sometimes Eq. 22-15 is called the variational derivative
of ![]() .6When the variational derivative vanishes,
.6When the variational derivative vanishes, ![]() is an extremal
function and a candidate for a local maximum or minimum.
For the case of the gradient energy, if Eq. 22-15 vanishes,
then
is an extremal
function and a candidate for a local maximum or minimum.
For the case of the gradient energy, if Eq. 22-15 vanishes,
then ![]() is an equilibrium profile.
is an equilibrium profile.
The functional gradient is the starting point for the kinetic equations for conserved and non-conserved parameter fields.
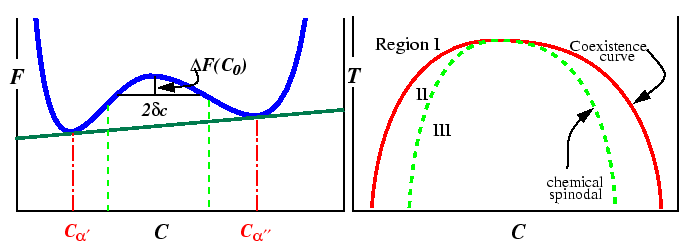
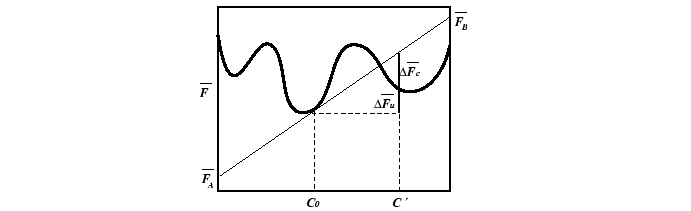
Appendix: Free Energy Changes and Geometric Constructions
The free energy versus composition curve, illustrated in the
above for a constant temperature,
is a familiar example of a free energy which
gives rise to a miscibility gap.
The region between the spinodal lines delimits those compositions for
which there is no barrier to decomposition.
Inside the miscibility gaps, but outside of the spinodal region, decomposition
is favored but a thermodynamic barrier requires large fluctuations in
composition (i.e., nucleation) for decomposition.
The position of spinodal lines is determined
by the sign of the free energy change for a small fluctuation in composition.
The following derivation is from Hilliard which derives
the variation of the molar free energy,
![]() ,
but this derivation applies
to any extensive molar quantity.7.
,
but this derivation applies
to any extensive molar quantity.7.
We can write
![]() in terms of its partial molar quantities,
in terms of its partial molar quantities,
![]() and
and
![]() :
:
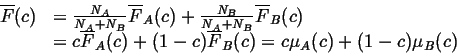 |
(22-16) |
| (22-17) |
 |
However, if the system is closed (which is the
case for a localized fluctuation in composition), then it is necessary to
account for the exchange of material necessary to satisfy the constraint
of fixed composition.
For each mole transformed, the change in
![]() for the
for the ![]() moles
of the
moles
of the ![]() component is
component is
![]() , with a
similar term for the
, with a
similar term for the ![]() component:
component:
| (22-18) |
![\begin{displaymath}\begin{array}{ll} \Delta \overline{F} = & c' \overline{F}_B(c...
... - c') [ \overline{F}_B(c_0) - \overline{F}_A(c_0)] \end{array}\end{displaymath}](img95.gif) |
(22-19) |
Consider the special case of a small composition fluctuation,
![]() .
Expanding
.
Expanding
![]() in
in ![]() :
:
Substituting Eq. 22-20 into Eq. 22-21 results in the
change in the molar free energy for a variation of a conserved
parameter ![]() :
:
Similarly, the lowest order term for the
change in the molar free energy for a variation of a non-conserved
order parameter ![]() is
is
Therefore, an order parameter can always decrease the free energy
by picking a variation
![]() with a sign that makes the product in
Eq. 22-23 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
with a sign that makes the product in
Eq. 22-23 negative.
An non-conserved order parameter has no barrier against reaching a
value which makes the free energy a local minimum.
On the other hand, for a conserved quantity like ![]() , the variation
in molar free energy is proportional to
, the variation
in molar free energy is proportional to
![]() .
Therefore, a barrier to the growth of small variations exists whenever
the second derivative in Eq. 22-22 is positive.
Thus, nucleation is required for a transformation outside of the
spinodal curves.
.
Therefore, a barrier to the growth of small variations exists whenever
the second derivative in Eq. 22-22 is positive.
Thus, nucleation is required for a transformation outside of the
spinodal curves.
The sign of Eq. 22-22
determines the sign of the interdiffusion coefficient.