... degree.''¹

Ibid Page 256, An fraction of the paragraph where this quote appears is so much fun, that I can't resist giving it here:

$ldots$ Another kind of change is conceivable, which initially is small in degree but may be great in its extent in space. Stability in this respect or stability in respect to continuous changes in phase has already been discussed (see page 105), and its limits determined. These limits depend entirely upon the fundamental equation of the homogeneous mass of which the stability is in question. But with respect to the kind of changes here considered, which are initially small in extent but great in degree, it does not appear how we can fix the limits of stability with the same precision. But it is safe to say that if there is such a limit it must be at or beyond the limit at which [surface tension] vanishes. This latter limit is determined by the fundamental equation of the [interface] between the the phase of which the stability is in question and that of which the possible formation is in question. $ldots$

It is interesting that Gibbs' initial considerations about stability--and admittedly more precise predictions--concerned the continuous phase transformation; subsequently, he worked out the conditions for nucleation. This is opposite to the order of historical and typically pedagogical approach in materials science.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

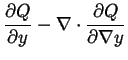
... expansion.²

The following example is taken from Landau and Lifshitz, ``Statistical Physics'' third edition, pages 451-455

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... $y(\vec{x})$³

A functional is a function of a function; in this case, it takes a function and maps it to a scalar which is numerically equal to the total free energy of the system

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... values⁴

If $y$ represents a conserved quantity like $c$, then the variation $vt$ must not contribute to the total content of the system ( $\int vt dV = 0$), but we will satisfy this requirement automatically below.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

....⁵

This is one particular choice for the functional gradient, for which there are an infinite number of choices. This particular choice (the gradient in the $L2$-norm of functions) describes the physics of the problem.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

....⁶

For the general functional, $P[y] = \int Q[y(\vec{x}),\nabla y] dV$, the variational derivative of $P$ is

$$\frac{\partial Q}{\partial y} - \nabla \cdot \frac{\partial Q}{\partial \nabla y}$$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... quantity.⁷

An extensive quantity is one which depend on the total size of a system, like the volume, enthalpy, or free energy. A molar extensive quantity is scaled by diving by the total number of moles in the system: $\overline{V}(c) = V(c)/(N_A + N_B) = \overline{V}(N_A/(N_A + N_B)) = \overline{V}(\overline{N}_A)$. A molal extensive quantity is scaled by dividing by the number of moles of a particular species.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.