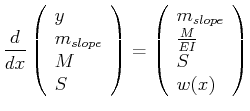Next: Linearization of Systems of ODEs
Up: Lecture_24_web
Previous: Systems of Ordinary Differential Equations
Next: Linearization of Systems of ODEs
Up: Lecture_24_web
Previous: Systems of Ordinary Differential Equations
Higher-order ordinary differential equations can usually be re-written
as a system of first-order differential equations.
If the higher-order ODE can be solved for its largest derivative:
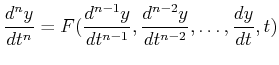 |
(24-6) |
then 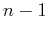 ``new'' functions can be introduced via
``new'' functions can be introduced via
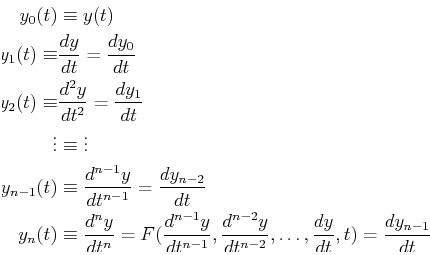 |
(24-7) |
or
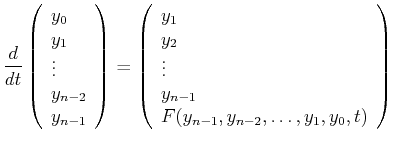 |
(24-8) |
For example, the damped harmonic oscillator,
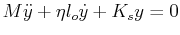 , can be re-written
by introducing the momentum variable,
, can be re-written
by introducing the momentum variable,
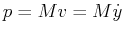 , as the
system:
, as the
system:
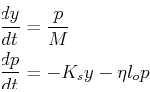 |
(24-9) |
which has only one critical point 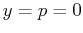 .
.
The equation for a free pendulum,
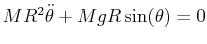 ,
can be re-written by introducing the angular momentum variable,
,
can be re-written by introducing the angular momentum variable,
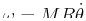 as the system,
as the system,
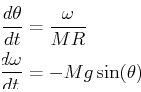 |
(24-10) |
which has two different kinds of critical points:
(
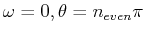 ) and
(
) and
(
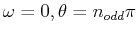 ).
).
Finally, the beam equation
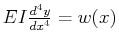 can be rewritten
as the system:
can be rewritten
as the system:
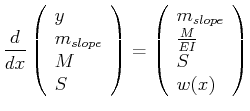 |
(24-11) |
where 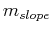 is the slope of the beam,
is the slope of the beam,
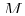 is the local bending moment in the beam,
is the local bending moment in the beam,
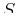 is the local shearing force in the beam,
and
is the local shearing force in the beam,
and 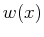 is the load density.
is the load density.
This beam equation does not have any interesting critical points.
© W. Craig Carter 2003-, Massachusetts Institute of Technology
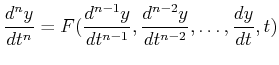
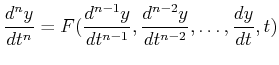
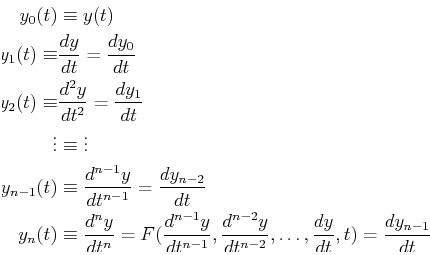
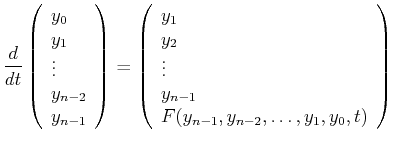
![]() , can be re-written
by introducing the momentum variable,
, can be re-written
by introducing the momentum variable,
![]() , as the
system:
, as the
system:
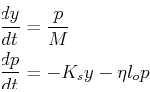
![]() ,
can be re-written by introducing the angular momentum variable,
,
can be re-written by introducing the angular momentum variable,
![]() as the system,
as the system,
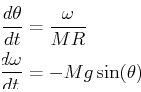
![]() can be rewritten
as the system:
can be rewritten
as the system: