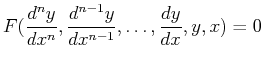 |
(24-1) |
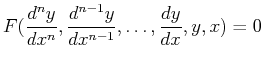 |
(24-1) |
The predator-prey model serves as the classical example of a system of differential equations.
|
MATHEMATICA |
| (notebook Lecture-24) |
| (html Lecture-24) |
| (xml+mathml Lecture-24) |
| An iterative example of a predator-prey problem with a slight twist.
Suppose there is a fairly bad joke that circulates around the student
population.
Students either know the joke or they don't.
Of course, freshman enter a constant rate
It is closely held secret that Susan Hockfield, MIT's president, has an odd sense of humor. At each commencement ceremony, as the proud candidates for graduation approach the president to collect their hard-earned diploma, President Hockfield whispers to the student, ``Have you the joke about?'' If the student says, ``Yes. I have heard that joke. It is very funny!!!'' then the diploma is awarded. However, if the student says, ``No. But, I am dying to hear it!!!'', the president's face drops into a sad frown and the student is asked to leave without collecting the diploma.1 Therefore, an iterative model for the student population that knows the joke is:
Naive Fraction
Jaded Fraction
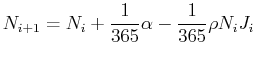
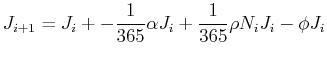
|
The
MATHEMATICA![]() example could be modeled with the set of differential equations:
example could be modeled with the set of differential equations:
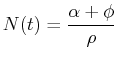 and and 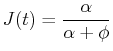 |
(24-5) |