Link to Current (updated) notes

Next: Fourth Order ODEs, Elastic Beams Up: Lecture_21_web Previous: Second Order ODEs with Constant Coefficients

Boundary Value Problems

It has been shown that all solutions to $\ensuremath{\frac{d^2{y}}{d{x}^2}} + \beta \ensuremath{\frac{d{y}}{d{x}}} + \gamma y = 0$ can be determined from a linear combination of the basis solution. Disregard for a moment whether the solution is complex or real, and ignoring the special case $\gamma = (\beta/2)^2$ . The solution to any problem is given by

$\displaystyle y(x) = C_+ e^{\lambda_+ x} + C_- e^{\lambda_- x}$

(21-14)

How is a solution found for a particular problem? Recall that two values must be specified to get a solution--these two values are just enough so that the two constants

and

can be obtained.

In many physical problems, these two conditions appear at the boundary of the domain. A typical problem is posed like this:

Solve

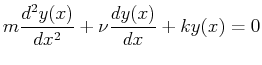$\displaystyle m \ensuremath{\frac{d^2{y(x)}}{d{x}^2}} + \nu \ensuremath{\frac{d{y(x)}}{d{x}}} + k y(x) = 0$ on $\displaystyle 0 < x < L$

(21-15)

subject to the boundary conditions

$\displaystyle y(x=0) = 0$ and $\displaystyle y(x=L) = 1$

or, solve

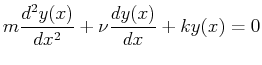$\displaystyle m \ensuremath{\frac{d^2{y(x)}}{d{x}^2}} + \nu \ensuremath{\frac{d{y(x)}}{d{x}}} + k y(x) = 0$ on $\displaystyle 0 < x < \infty$

(21-16)

subject to the boundary conditions

$\displaystyle y(x=0) = 1$ and $\displaystyle y'(x=L) = 0$

When the value of the function is specified at a point, these are called Dirichlet conditions; when the derivative is specified, the boundary condition is called a Neumann condition. It is possible have boundary conditions that are mixtures of Dirichlet and Neumann.

MATHEMATICA $^{\text{\scriptsize {\textregistered }}}$ Example

(notebook Lecture-21)

(html Lecture-21)

(xml+mathml Lecture-21)

Determining Solution Constants from Boundary Values

Using Solve, find the specific solution to and .
Using Solve, find the specific solution to and .

When the domain is infinite or semi-infinite and the physical situation indicates that the solution must be bounded, then one can automatically set the constants associated with roots with real positive parts to zero, because these solutions grow without bound.