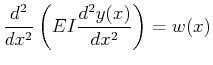 |
(21-17) |
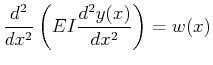 |
(21-17) |
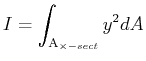 |
(21-18) |
If the moment of inertia and the Young's modulus do not depend on the position in the beam (the case for a uniform beam of homogeneous material), then the beam equation becomes:
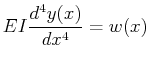 |
(21-19) |
The homogeneous solution can be obtained by inspection--it is
a general cubic equation
![]() which has the four
constants that are expected from a fourth-order ODE.
which has the four
constants that are expected from a fourth-order ODE.
The particular solution can be obtained by integrating ![]() four
times--if the constants of integration are included then the
particular solution naturally contains the homogeneous solution.
four
times--if the constants of integration are included then the
particular solution naturally contains the homogeneous solution.
The load density can be discontinuous or it can contain Dirac-delta
functions
![]() representing a point load
representing a point load ![]() applied
at
applied
at ![]() .
.
It remains to determine the constants from boundary conditions.
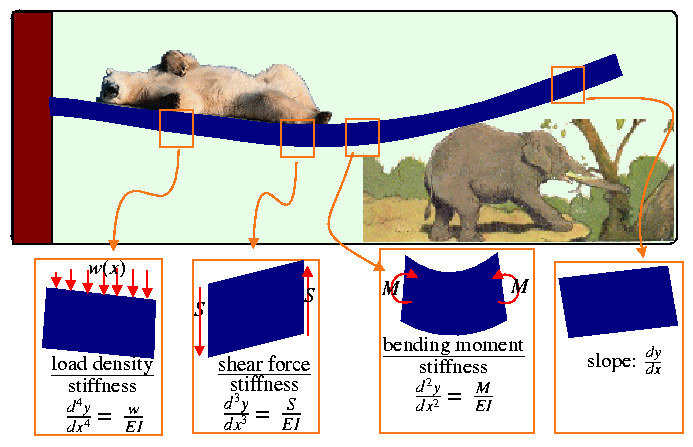
The boundary conditions can be determined because each derivative
of ![]() has a specific meaning as illustrated in Fig. 21-2.
has a specific meaning as illustrated in Fig. 21-2.
|
|
There are common loading conditions that determine boundary conditions:
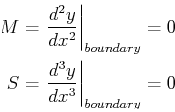
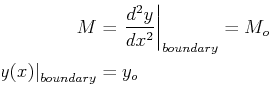
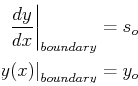
|
MATHEMATICA |
| (notebook Lecture-23) |
| (html Lecture-23) |
| (xml+mathml Lecture-23) |
| Visualizing beam deflections |