For first-order ordinary differential equations (ODEs),
![]() ,
one value
,
one value ![]() was needed to specify a particular solution.
For second-order equations, two independent values are needed.
This is illustrated in the following forward-differencing example.
was needed to specify a particular solution.
For second-order equations, two independent values are needed.
This is illustrated in the following forward-differencing example.
|
MATHEMATICA |
| (notebook Lecture-21) |
| (html Lecture-21) |
| (xml+mathml Lecture-21) |
| A Second-Order Forward Differencing Example
Recall the example in Lecture 19 of a first-order differencing scheme: at each iteration the function grew proportionally to its current size. In the limit of very small forward differences, the scheme converged to exponential growth. Now consider a situation in which function's current rate of growth increases proportionally to two terms: its current rate of growth and its size.
Change in Value's Rate of Change
To Calculate a forward differencing scheme for this case, let
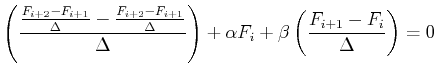
and then solve for the ``next increment''
|
Therefore, a linear heterogeneous ordinary differential equation
can be written as a product of general functions of the
dependent variable and the derivatives for the ![]() -order linear
case:
-order linear
case:
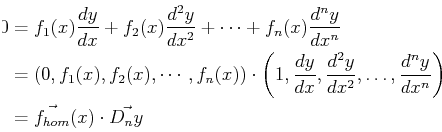 |
(21-2) |
Equation 21-1 can always be multiplied by
![]() to generate the general form:
to generate the general form:
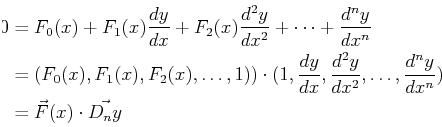 |
(21-3) |
For the second-order linear ODE, the heterogeneous form can always be written as:
Because two values must be specified for each solution to a second order equation--the solution can be broken into two basic parts, each deriving from a different constant. These two independent solutions form a basis pair for any other solution to the homogeneous second-order linear ODE that derives from any other pair of specified values.
The idea is the following:
suppose the solution to Eq. 21-5
is found the particular case of specified parameters
![]() and
and
![]() , the solution
, the solution
![]() can be written
as the sum of solutions to two other problems.
can be written
as the sum of solutions to two other problems.
| (21-6) |
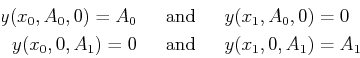 |
(21-7) |
The two arbitrary integration constants can be included in the definition of the general solution:
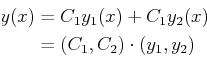 |
(21-8) |