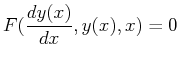 |
(19-4) |
The relationship between a function and its derivatives for a first-order ODE,
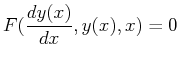 |
(19-4) |
If ![]() can be solved for exactly,
can be solved for exactly,
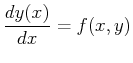 |
(19-5) |
|
MATHEMATICA |
| (notebook Lecture-19) |
| (html Lecture-19) |
| (xml+mathml Lecture-19) |
| The Geometry of First-Order ODES: Examples
Consider Newton's law of cooling that states that the rate that a body cools by radiation is proportional to the difference in temperature between the body and its surroundings:
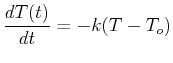
Make the equation simpler by converting to a non-dimensional form, let
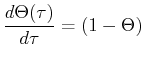
|