If a first-order ordinary
differential equation
![]() can be rearranged so that
only one variable, for instance
can be rearranged so that
only one variable, for instance ![]() , appears on the left-hand-side multiplying
its derivative and
the other,
, appears on the left-hand-side multiplying
its derivative and
the other, ![]() , appears only on the right-hand-side, then the
equation is said to be `separated.''
, appears only on the right-hand-side, then the
equation is said to be `separated.''
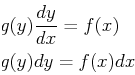 |
(19-6) |
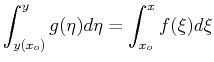 |
(19-7) |
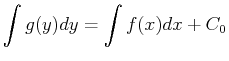 |
(19-8) |
|
MATHEMATICA |
| (notebook Lecture-19) |
| (html Lecture-19) |
| (xml+mathml Lecture-19) |
| Using
MATHEMATICA
MATHEMATICA |
While the accuracy of the first-order differencing scheme can
be determined by comparison to an exact solution, the question
remains of how to establish accuracy and convergence
with the step-size ![]() for an arbitrary ODE.
This is a question of primary importance and studied by
Numerical Analysis.
for an arbitrary ODE.
This is a question of primary importance and studied by
Numerical Analysis.