Link to Current (updated) notes

Other forms of the Fourier coefficients

Sometimes the primary domain is defined with a different starting point and different symbols, for instance Kreyszig uses a centered domain by using $-L$ as the starting point and $2 L$ as the period, and in these cases the forms for the Fourier coefficients look a bit different. One needs to look at the domain in order to determine which form of the formulas to use.

Extra Information and Notes
Potentially interesting but currently unnecessary

The ``trick'' of multiplying both sides of Eq. 17-8 by a function and integrating comes from the fact that the trigonometric functions form an orthogonal basis for functions with inner product defined by

$$f(x) \cdot g(x) = \int_0^\lambda f(x) g(x) dx$$

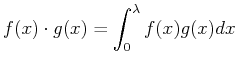
Considering the trigonometric functions as components of a vector:

$$\begin{split} \vec{e_0}(x) = & (1, 0, 0, \ldots , )\\ \vec{... ...e_n}(x) = & (\ldots \ldots, \sin(k_n x), \ldots , ) \end{split}$$

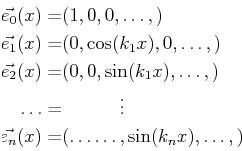
then these ``basis vectors'' satisfy $\vec{e_i} \cdot \vec{e_j} = (\lambda/2) \delta_{ij}$ , where $\delta_{ij} = 0$ unless $i=j$ . The trick is just that, for an arbitrary function represented by the basis vectors, $\vec{P}(x) \cdot \vec{e_j}(x) = (\lambda/2) P_j$ .