The functions
![]() and
and
![]() each have period
each have period ![]() .
That is, they each take on the same value at
.
That is, they each take on the same value at ![]() and
and
![]() .
.
There are an infinite number of other simple trigonometric functions
that are periodic in ![]() ; they are
; they are
![]() and
and
![]() and
which cycle two times
within each
and
which cycle two times
within each ![]() ,
,
![]() and
and
![]() and
which cycle three times
within each
and
which cycle three times
within each ![]() , and, in general,
, and, in general,
![]() and
and
![]() and
which cycle
and
which cycle ![]() times
within each
times
within each ![]() .
.
The constant function,
![]() const
, also satisfies
the periodicity requirement.
const
, also satisfies
the periodicity requirement.
The superposition of multiples of any number of periodic function
must also be a periodic function, therefore any function ![]() that
satisfies:
that
satisfies:
If any periodic function ![]() could be represented by the series in
in Eq. 17-8 by a suitable choice of coefficients, then
an alternative representation of the periodic function could be
obtained in terms of the simple trigonometric functions and their
amplitudes.
could be represented by the series in
in Eq. 17-8 by a suitable choice of coefficients, then
an alternative representation of the periodic function could be
obtained in terms of the simple trigonometric functions and their
amplitudes.
The ``inverse question'' remains: ``How are the amplitudes
![]() (the even trigonometric terms) and
(the even trigonometric terms) and
![]() (the odd trigonometric terms) determined
for a given
(the odd trigonometric terms) determined
for a given ![]() ?''
?''
The method follows from what appears to be a ``trick.''
The following three integrals have simple forms for integers ![]() and
and ![]() :
:
Therefore, any amplitude can be determined by multiplying both sides of
Eq. 17-8 by
its conjugate trigonometric function and integrating over the domain.
(Here we pick the domain to start at zero,
![]() ,
but any other starting point would work fine.)
,
but any other starting point would work fine.)
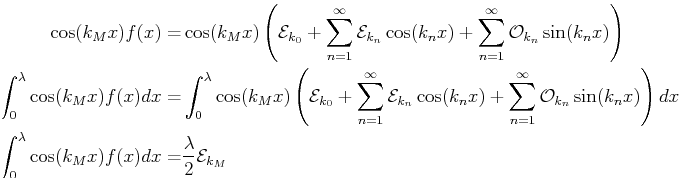 |
(17-10) |
The constant term has an extra factor of two because
![]() instead of the
instead of the ![]() found in Eq. 17-9.
found in Eq. 17-9.
|
MATHEMATICA |
| (notebook Lecture-17) |
| (html Lecture-17) |
| (xml+mathml Lecture-17) |
| Orthogonality of Trignometric Functions
Demonstrate that the relations in Eq. 17-9 are true.
MATHEMATICA Calculating Fourier Amplitudes
|