A Taylor expansion approximates the behavior of a suitably defined
function, ![]() in the neighborhood of a point,
in the neighborhood of a point, ![]() ,
with a bunch of functions,
,
with a bunch of functions, ![]() ,
defined by the set of powers:
,
defined by the set of powers:
| (17-5) |
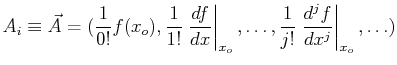 |
(17-7) |
However, for periodic functions, the domain over which the approximation is required is only one period of the periodic function--the rest of the function is taken care of by the definition of periodicity in the function.
Because the function is periodic, it makes sense to use functions
that have the same period to approximate it.
The simplest periodic functions are the trigonometric functions.
If the period is ![]() , any other periodic function with
periods
, any other periodic function with
periods ![]() ,
, ![]() ,
, ![]() , will also have
period
, will also have
period ![]() .
Using these "sub-periodic" trigonometric functions is the idea
behind Fourier Series.
.
Using these "sub-periodic" trigonometric functions is the idea
behind Fourier Series.