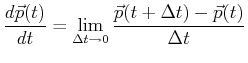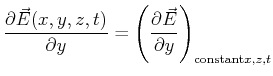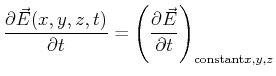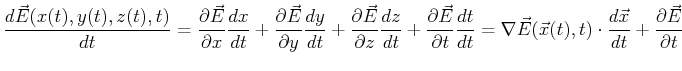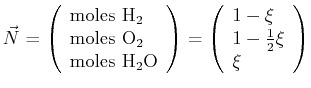Next: Index
Up: Lecture_11_web
Previous: Vector Products
Next: Index
Up: Lecture_11_web
Previous: Vector Products
Subsections
Consider a vector, 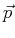 , as a point in space.
If that vector is a function of a real
continuous parameter for instance,
, as a point in space.
If that vector is a function of a real
continuous parameter for instance, 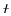 ,
then
,
then
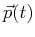 represents the
loci as a function of a parameter.
represents the
loci as a function of a parameter.
If
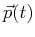 is continuous, then it sweeps out
a continuous curve as
is continuous, then it sweeps out
a continuous curve as 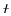 changes continuously.
It is very natural to think of
changes continuously.
It is very natural to think of 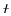 as time and
as time and
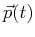 as the trajectory of a particle--such a trajectory would
be continuous if the particle does not disappear at one
instant,
as the trajectory of a particle--such a trajectory would
be continuous if the particle does not disappear at one
instant, 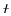 , and reappear an instant later,
, and reappear an instant later, 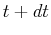 ,
some finite distance distance away from
,
some finite distance distance away from
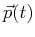 .
.
If
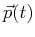 is continuous, then the limit:
is continuous, then the limit:
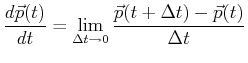 |
(11-5) |
Notice that the numerator inside the limit is a vector and
the denominator is a scalar;
so, the derivative is also a vector.
Think about the equation geometrically--it should be apparent
that the vector represented by the derivative is locally tangent
to the curve that is traced out by the points
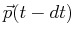 ,
,
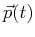
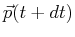 , etc.
, etc.
Review: Partial and total derivatives
One might also consider a time- and space-dependent vector field, for
instance
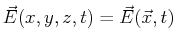 could be the
force on a unit charge located at
could be the
force on a unit charge located at 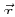 at time
at time 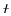 .
.
Here, there are many different things which might be varied and
give rise to a derivative.
Such questions might be:
- How does the force on a unit charge differ for two nearby
unit-charge particles, say at
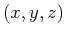 and at
and at
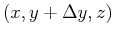 ?
?
- How does the force on a unit charge located at
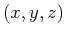 vary
with time?
vary
with time?
- How does the the force on a particle change as the
particle traverses some path
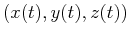 in space?
in space?
Each question has the ``flavor'' of a derivative, but each is
asking a different question.
So a different kind of derivative should exist for each type
of question.
The first two questions are of the nature, ``How does a quantity
change if only one of its variables changes and the others are
held fixed?''
The kind of derivative that applies is the partial derivative.
The last question is of the nature, ``How does a quantity change
when all of its variables depend on a single variable?''
The kind of derivative that applies is the total derivative.
The answers are:
-
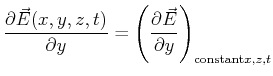 |
(11-6) |
-
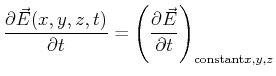 |
(11-7) |
-
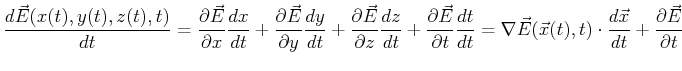 |
(11-8) |
It is useful to think of vectors as spatial objects when
learning about them--but one shouldn't get stuck with the
idea that all vectors are points in two- or three-dimensional
space.
The spatial vectors serve as a good analogy to generalize
an idea.
For example,
consider the following chemical reaction:
| Reaction: |
H
|
 O O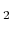
|
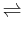
|
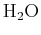
|
| Initial: |
1 |
1 |
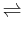
|
0 |
| During Rx.: |
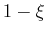
|
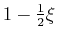
|
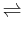
|
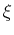
|
The composition could be written as a vector:
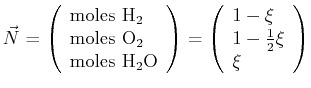 |
(11-9) |
and the variable 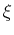 plays the role of the ``extent'' of the
reaction--so the composition variable
plays the role of the ``extent'' of the
reaction--so the composition variable 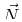 lives in
a reaction-extent (
lives in
a reaction-extent ( ) space of chemical species.
) space of chemical species.
© W. Craig Carter 2003-, Massachusetts Institute of Technology
![]() is continuous, then it sweeps out
a continuous curve as
is continuous, then it sweeps out
a continuous curve as ![]() changes continuously.
It is very natural to think of
changes continuously.
It is very natural to think of ![]() as time and
as time and
![]() as the trajectory of a particle--such a trajectory would
be continuous if the particle does not disappear at one
instant,
as the trajectory of a particle--such a trajectory would
be continuous if the particle does not disappear at one
instant, ![]() , and reappear an instant later,
, and reappear an instant later, ![]() ,
some finite distance distance away from
,
some finite distance distance away from
![]() .
.
![]() is continuous, then the limit:
is continuous, then the limit: