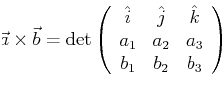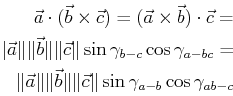Next: Derivatives Vectors
Up: Lecture_11_web
Previous: Lecture_11_web
Next: Derivatives Vectors
Up: Lecture_11_web
Previous: Lecture_11_web
Subsections
The concept of vectors as abstract objects representing
a collection of data has already been presented.
Every student at this point has already encountered vectors
as representation of points, forces, and accelerations in
two and three dimensions.
MATHEMATICA Example
Example |
| (notebook Lecture-11) |
| (html Lecture-11) |
| (xml+mathml Lecture-11) |
Solution to 2D Diffusion Equation for Point Source Initial Conditions
|
An inner (or dot-) project is multiplication of two vectors that
produces a scalar.
 |
(11-1) |
The inner product is:
- linear, distributive
-
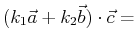
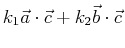
- symmetric
-
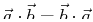
- satifies Schwarz inequality
-
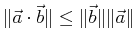
- satifies triangle inequality
-
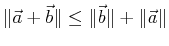
If
the vector components are in a cartesian (i.e., cubic lattice) space,
then there is a useful equation for the angle
between two vectors:
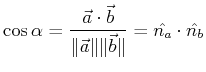 |
(11-2) |
where 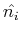 is the unit vector that shares a direction with
is the unit vector that shares a direction with 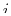 .
Caution: when working with vectors in non-cubic crystal
lattices (e.g, tetragonal, hexagonal, etc.) the angle relationship above
does not hold.
One must convert to a cubic system first to calculate the angles.
.
Caution: when working with vectors in non-cubic crystal
lattices (e.g, tetragonal, hexagonal, etc.) the angle relationship above
does not hold.
One must convert to a cubic system first to calculate the angles.
The projection of a vector onto a direction  is a scalar:
is a scalar:
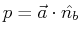 |
(11-3) |
The vector product (or cross  ) differs from the dot (or inner) product
in that multiplication produces a vector from two vectors.
One might have quite a few choices about how to define
such a product, but the following idea proves to be
useful (and standard).
) differs from the dot (or inner) product
in that multiplication produces a vector from two vectors.
One might have quite a few choices about how to define
such a product, but the following idea proves to be
useful (and standard).
- normal
- Which way should the product vector point?
Because two vectors (usually) define a plane, the product
vector might as well point away from it.
The exception is when the two vectors are linearly dependent;
in this case the product vector will have zero magnitude.
The product vector is normal to the plane defined by
the two vectors that make up the product.
A plane has two normals, which normal should be picked?
By convention, the ``right-hand-rule'' defines which of
the two normal should be picked.
- magnitude
- Given that the product vector points away from the two
vectors that make up the product, what should be its
magnitude?
We already have a rule that gives us the cosine of the angle
between two vectors, a rule that gives the sine of the
angle between the two vectors would be useful.
Therefore, the cross product is defined so that its magnitude for two
unit vectors is the sine of the angle between them.
This has the extra utility that the cross product is zero when
two vectors are linearly-dependent (i.e., they do not define
a plane).
This also has the utility, discussed below, that the triple
product will be a scalar quantity equal to the volume
of the parallelepiped defined by three vectors.
The triple product,
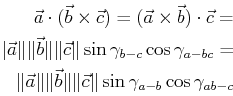 |
(11-4) |
where
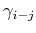 is the angle between two vectors
is the angle between two vectors 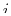 and
and 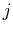 and
and
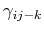 is the angle between the vector
is the angle between the vector 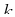 and plane spanned by
and plane spanned by
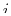 and
and 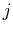 .
is equal to the parallelepiped that has
.
is equal to the parallelepiped that has 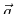 ,
, 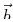 , and
, and 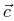 ,
emanating from its bottom-back corner.
,
emanating from its bottom-back corner.
If the triple product is zero, the volume between three vectors is
zero and therefore they must be linearly dependent.
© W. Craig Carter 2003-, Massachusetts Institute of Technology
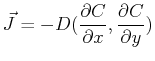
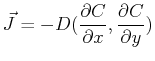

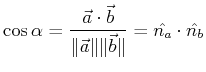
![]() is a scalar:
is a scalar: