Next: Index
Up: Lecture_10_web
Previous: Quadratic Forms
Next: Index
Up: Lecture_10_web
Previous: Quadratic Forms
Among all similar matrices (defined by the similarity transformation
defined by Eq. 10-13), the simplest matrix is the
diagonal one.
In the coordinate system where the similar matrix is diagonal, its
diagonal entries are the eigenvalues.
The question remains, ``what is the coordinate transformation
that takes the matrix into its diagonal form?''
The coordinate system is called the eigenbasis or principal axis
system, and the transformation that takes it there is particularly
simple.
The matrix that transforms from a general (old) coordinate
system to a diagonalized matrix (in the new coordinate system)
is the matrix of columns of the eigenvectors.
The first column corresponds to the first eigenvalue on
the diagonal matrix, and the 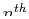 column is the
eigenvector corresponding the
column is the
eigenvector corresponding the 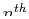 eigenvalue.
eigenvalue.
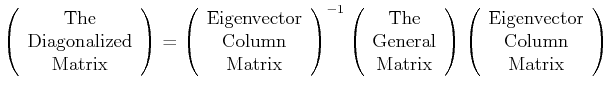 |
(10-29) |
This method provides a method for finding the
simplest quadratic form.
© W. Craig Carter 2003-, Massachusetts Institute of Technology
![]() column is the
eigenvector corresponding the
column is the
eigenvector corresponding the ![]() eigenvalue.
eigenvalue.