
 Next: Eigenvector Basis
Up: Lecture_10_web
Previous: Similarity Transformations
Next: Eigenvector Basis
Up: Lecture_10_web
Previous: Similarity Transformations
The example above, where a matrix (rank-2 tensor) represents
a material property, can be understood with a useful geometrical
interpretation.
For the case of the conductivity tensor
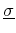 , the dot product
, the dot product
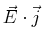 is a scalar related to the local energy dissipation:
is a scalar related to the local energy dissipation:
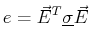 |
(10-21) |
The term on the right-hand-side is called a quadratic form, as
it can be written as:
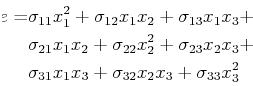 |
(10-22) |
or, because
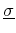 is symmetric:
is symmetric:
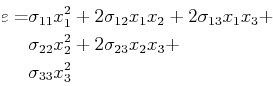 |
(10-23) |
It is not unusual for such quadratic forms to represent energy
quantities.
For the case of paramagnetic and diamagnetic materials
with magnetic permeability tensor
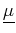 , the energy
per unit volume due to an applied magnetic field
, the energy
per unit volume due to an applied magnetic field 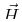 is:
is:
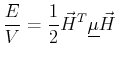 |
(10-24) |
for a dielectric (i.e., polarizable) material with electric
electric permittivity tensor
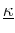 with an applied
electric field
with an applied
electric field 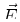 :
:
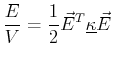 |
(10-25) |
The geometric interpretation of the quadratic forms is obtained
by turning the above equations around and asking--what are
the general vectors 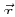 for which the quadratic form
(usually an energy or power density) has a particular value?
Picking that particular value as unity, the question becomes
what are the directions and magnitudes of
for which the quadratic form
(usually an energy or power density) has a particular value?
Picking that particular value as unity, the question becomes
what are the directions and magnitudes of 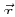 for which
for which
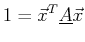 |
(10-26) |
This equation expresses a quadratic relationship between one component of
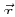 and the others.
This is a surface--known as the quadric surface
or representation quadric--which is an
ellipsoid or hyperboloid sheet on which the quadratic form takes
on the particular value 1.
and the others.
This is a surface--known as the quadric surface
or representation quadric--which is an
ellipsoid or hyperboloid sheet on which the quadratic form takes
on the particular value 1.
In the principal axes (or, equivalently, the eigenbasis) the
quadratic form takes the
quadratic form takes the simple form:
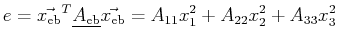 |
(10-27) |
and the representation quadric
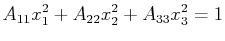 |
(10-28) |
which is easily characterized by the signs of the coefficients.
In other words, in the principal axis system (or the eigenbasis)
the quadratic form has a particularly simple, in fact the most
simple, form.
© W. Craig Carter 2003-, Massachusetts Institute of Technology
![]() , the dot product
, the dot product
![]() is a scalar related to the local energy dissipation:
is a scalar related to the local energy dissipation:
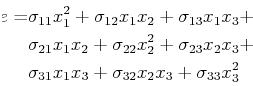
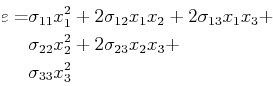
![]() , the energy
per unit volume due to an applied magnetic field
, the energy
per unit volume due to an applied magnetic field ![]() is:
is:
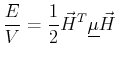
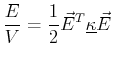
![]() for which the quadratic form
(usually an energy or power density) has a particular value?
Picking that particular value as unity, the question becomes
what are the directions and magnitudes of
for which the quadratic form
(usually an energy or power density) has a particular value?
Picking that particular value as unity, the question becomes
what are the directions and magnitudes of ![]() for which
for which