Consider methane (
CH![]() ),
propane (
C
),
propane (
C![]() H
H![]() ),
and butane (
C
),
and butane (
C![]() H
H![]() ).
).
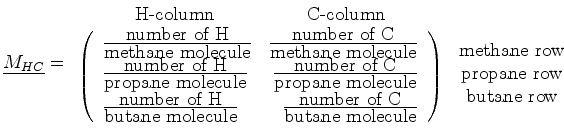 |
(06-11) |
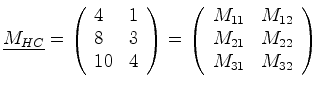 |
(06-12) |
| (06-13) | ||
| (06-14) | ||
| (06-15) |
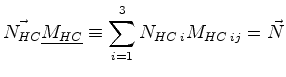 |
(06-16) |
The ``summation'' convention is often used, where a repeated index is summed over all its possible values:
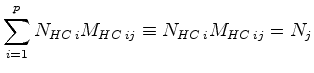 |
(06-17) |
For example, suppose
| (06-18) |
 |
(06-19) |
Above the lists (or vectors) of atoms were stored as rows, often it is convenient to store them as columns. The operation to take a row to a column (and vice-versa) is a ``transpose''.
 |
(06-20) |
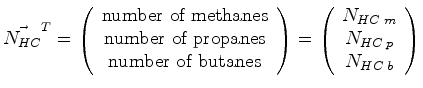 |
(06-21) |
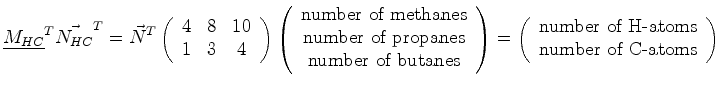 |
(06-22) |
|
MATHEMATICA |
||||||||
| (notebook Lecture-06) | ||||||||
| (html Lecture-06) | ||||||||
| (xml+mathml Lecture-06) | ||||||||
| Matrices
Suppose that some process that produces hyrdocarbons
can be modeled with the pressure
or
Then, if we wanted to find an operation that takes us from
the processing vector
Using matrix multiplication,
is a matrix, which when operating on a vector of pressure and temperature, returns a vector of the amount of hydrogen and carbon. |
Matrix multiplication is defined by:
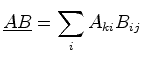 |
(06-27) |
Sometimes what we wish to know, ``What vector is it (![]() ),
when transformed by some matrix (
),
when transformed by some matrix (![]() ) gives us a particular
result (
) gives us a particular
result (
![]() )?''
)?''
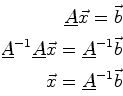 |
(06-28) |
The inverse of a matrix is defined as something that when multiplied with the matrix leaves a product that has no effect on any vector. This special product matrix is called the identidy matrix.
|
MATHEMATICA |
||||
| (notebook Lecture-04) | ||||
| (html Lecture-04) | ||||
| (xml+mathml Lecture-04) | ||||
| Inverting Matrices
where
|
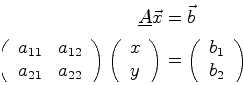 |
(06-31) |

|
MATHEMATICA |
||
| (notebook Lecture-06) | ||
| (html Lecture-06) | ||
| (xml+mathml Lecture-06) | ||
| Eliminating redundant equations or variables
Consider liquid water near the freezing point--dipole interactions
will tend to make water molecules form clusters such as
H Then the mapping from molecules to the number of atoms becomes:
|