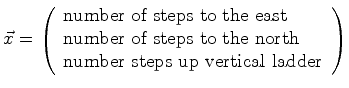 |
(06-1) |
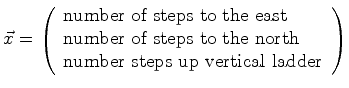 |
(06-1) |
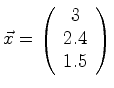 |
determines position |  |
(06-2) |
The vector above is just one example of a position vector.
We could also use coordinate systems that differ
from the Cartesian ![]() to represent
the location.
For example, the location in cylindrical coordinate system could
be written as
to represent
the location.
For example, the location in cylindrical coordinate system could
be written as
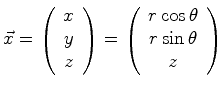 |
(06-3) |
The position could also be written as a cylindrical, or polar vector
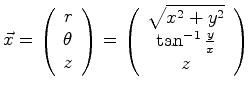 |
(06-4) |
However, vectors need not represent position at all, for example:
 |
(06-5) |
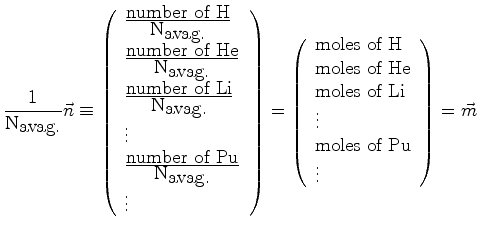 |
(06-6) |
| (06-7) | ||
| (06-8) |
| unit direction vector | mole fraction composition | (06-9) | |
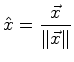 |
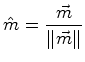 |
(06-10) |
| Extra Information and Notes
Potentially interesting but currently unnecessary |
| If
For the unit (direction) vector:
For the case of the composition vector, it is strange to consider
the case of a negative number of atoms, so the mole fraction
vector
|