

Next: Classifying the Invariant Points:
Up: Lecture_30_web
Previous: Construction of Phase Diagrams
The phase diagram in Figure 30-4 is the simplest possible
two-component phase diagram at constant
pressure.
Figure:
The so-called "lens" phase diagram.
The upper line is the limit of
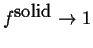 and is called called the solidus curve. The lower
line is called the liquidus curve.
and is called called the solidus curve. The lower
line is called the liquidus curve.
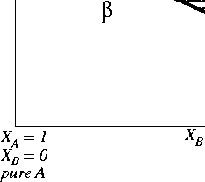 |
Figure 30-6:
A variation on the lens phase diagram.
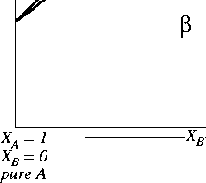 |
Consider how the Gibbs phase rule relates to the above phase diagrams.
The Gibbs phase rule is:
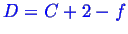
However,
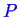 is constant so we lose one degree of freedom:
is constant so we lose one degree of freedom:
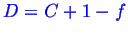
In the two phase region--
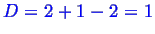 --so there
is one degree of freedom.
--so there
is one degree of freedom.
Question: What is the degree of freedom? What does it mean?
Consider another two-component phase
diagram and see if it violates the Gibbs
phase rule.
Figure 30-7:
Is this a possible phase diagram?
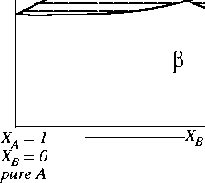 |
Consider the three-phase region:
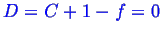
Because there are no degrees of freedom, the three-phase region
must shrink to a point in a two component system. This
places restrictions on the topology of binary
phase diagrams.
The diagrams below illustrate how such an invariant point (i.e., three
phase equilibria in a two component system) arises:
Figure 30-8:
Liquid is stable at all compositions at this temperature.
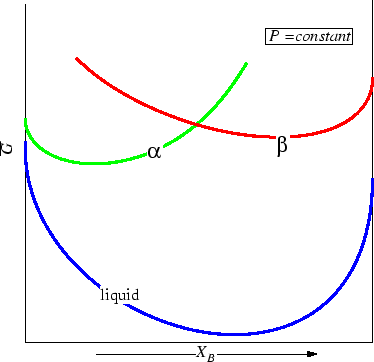 |
Figure 30-9:
One of the solid phases becomes stable.
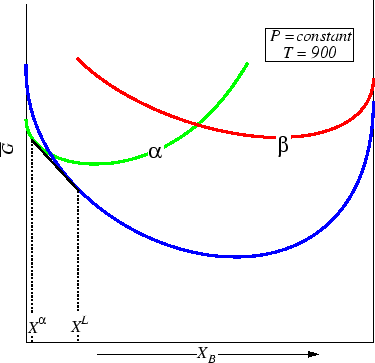 |
Figure 30-10:
The second solid phase becomes stable as well, but
not at the same compositions as the first.
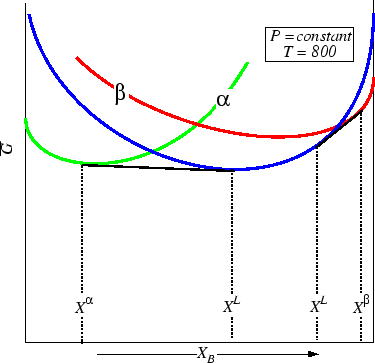 |
Figure 30-11:
At one unique temperature (the Eutectic) the two phase
regions converge-this is the invariant point.
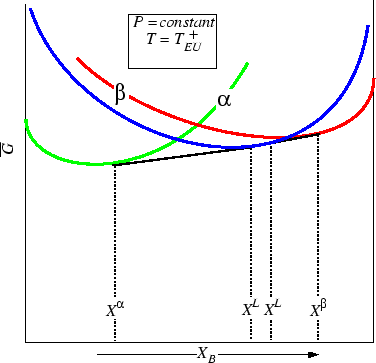 |
Figure 30-12:
Below the eutectic, the two solid phases are separated by
a two-phase region.
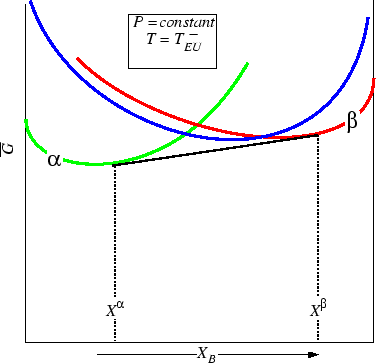 |
This yields the following phase diagram
Figure 30-13:
The free curves from Figures 30-8 through
30-12, result in a eutectic phase diagram.
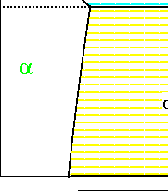 |


Next: Classifying the Invariant Points:
Up: Lecture_30_web
Previous: Construction of Phase Diagrams
W. Craig Carter
2002-12-03
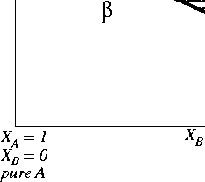
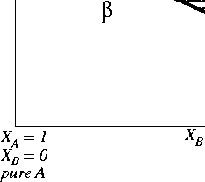
![]()
![]() is constant so we lose one degree of freedom:
is constant so we lose one degree of freedom:
![]()
![]() --so there
is one degree of freedom.
--so there
is one degree of freedom.
![]()

