

Next: About this document ...
Up: Lecture_28_web
Previous: Graphical Constructions for the
To calculate the equilibrium condition between several phases,
the condition that the chemical potential of each component
 is the same in each phase.
The graphical construction for chemical potential can be used
to obtain this condition--this condition will be called the
``common tangent'' condition.
is the same in each phase.
The graphical construction for chemical potential can be used
to obtain this condition--this condition will be called the
``common tangent'' condition.
Suppose another curve corresponding to
another phase that can also form a solution
of
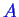 -
-
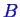 is considered.
Below, another graphical construction will be
demonstrated that will determine the properties
of stable phases.
is considered.
Below, another graphical construction will be
demonstrated that will determine the properties
of stable phases.
Consider two phases; to fix our ideas
let one curve be the molar Gibbs free energy
as a function of composition
at constant pressure and temperature
be for a solid solution.
Another curve for the liquid
solution will be added:
Figure 28-3:
Molar Gibbs Free Energies for a liquid
and solid solution at a particular pressure and temperature.
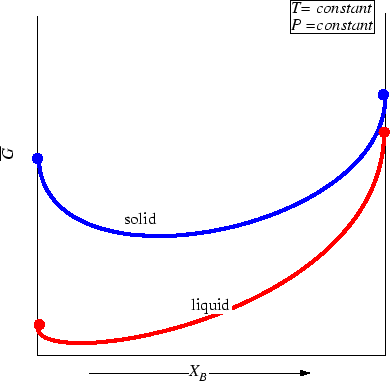 |
Questions:
- What is the molar free
energy charge for melting pure
 ? For
melting pure
? For
melting pure 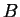 ?
?
- What is the molar free energy charge
for melting a solid solution at
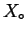 ?
?
- What is the free energy charge for
forming a liquid solution from
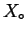 moles of pure
moles of pure 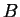 and
and
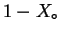 moles of
pure
moles of
pure  ?
?
- In the picture as it's drawn, rank
the following with respect to stability
from most stable to least stable at some fixed composition.
-
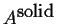 --
--
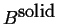
- A heterogeneous mixture of
pure solid
 and pure solid
and pure solid 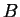 .
.
-
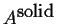 --
--
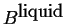
- Heterogeneous mixture of
pure solid
 and pure liquid
and pure liquid 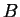 .
.
-
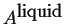 --
--
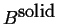
- A heterogeneous mixture of
pure liquid
 and pure solid
and pure solid 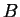 .
.
-
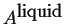 --
--
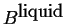
- A heterogeneous mixture of
pure liquid
 and pure liquid
and pure liquid 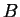 .
.
-
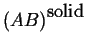
- Homogeneous solid solution of
 and
and 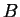 .
.
-
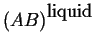
- Homogeneous liquid solution of
 and
and 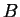 .
.
- Considering that
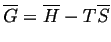 , which
curve will ``move'' the most as
, which
curve will ``move'' the most as 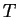 changes?
changes?
Consider the effect of lowering the temperature slightly.
Figure 28-4:
Figure 28-3 drawn at a slightly lower temperature.
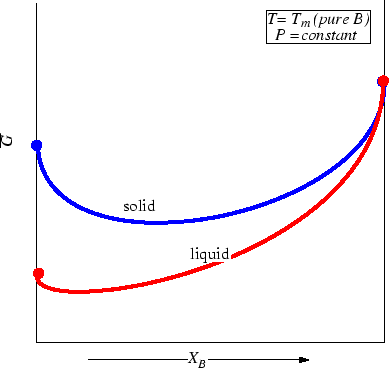 |
Figure 28-5:
Figure 28-4 drawn at an even lower temperature than
Figure 28-3.
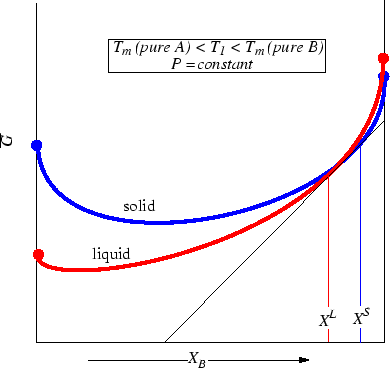 |
Question: Which combination is the most stable in Figure 28-5?
Hint: Consider that at
equilibrium
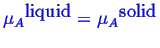 and
and
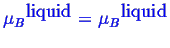


Next: About this document ...
Up: Lecture_28_web
Previous: Graphical Constructions for the
W. Craig Carter
2002-11-27
![]() is the same in each phase.
The graphical construction for chemical potential can be used
to obtain this condition--this condition will be called the
``common tangent'' condition.
is the same in each phase.
The graphical construction for chemical potential can be used
to obtain this condition--this condition will be called the
``common tangent'' condition.
![]() -
-
![]() is considered.
Below, another graphical construction will be
demonstrated that will determine the properties
of stable phases.
is considered.
Below, another graphical construction will be
demonstrated that will determine the properties
of stable phases.

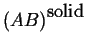
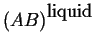
![]() and
and
![]()