Graphical Constructions for the Free Energy of Solutions

A useful graphical construction can be utilized for extracting values of chemical potentials:

Consider that the molar free energy of a solution is plotted as follows:

Figure 28-1: Example of the Molar Gibbs Free Energy of a Solution and related graphical constructions.

It would be particularly useful to obtain the chemical potentials of each species in solution as a function of composition. This relationship can be determined as follows:

Starting with an expression for the molar free energy of the solution being a weighted sum of the chemical potentials:

$$\ensuremath{\overline{G_{sol}}}= X_A\mu_A + X_B\mu_B$$ (28-5)

$d\ensuremath{\overline{G_{sol}}}$ becomes when using $dX_B = -dX_A$.

or

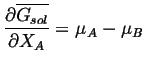$$\ensuremath{\frac{\partial{\ensuremath{\overline{G_{sol}}}}}{\partial{X_A}}}= \mu_A - \mu_B$$ (28-6)

at constant $P$ and $T$; similarly,

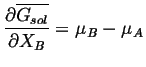$$\ensuremath{\frac{\partial{\ensuremath{\overline{G_{sol}}}}}{\partial{X_B}}}= \mu_B - \mu_A$$ (28-7)

Multiplying $\partial \ensuremath{\overline{G_{sol}}}/\partial X_B$ by $X_B$ and subtracting it from $\ensuremath{\overline{G_{sol}}}$:

$$\input{equations/20-6A}$$ (28-8)

or

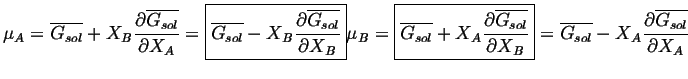$$\input{equations/intercept-const}$$ (28-9)

These equations can be interpreted with the following figure.

Figure: Illustration of how to determine the chemical potentials from a graph of $\ensuremath{\overline{G}}(X_B)$ for a binary alloy. $X_B^{arb}$ is an arbitrary composition where the tangent construction is performed.