Conditions for the Appearance of a New Phase

Last time, it was observed that a a soluble species (i.e, salt) cannot continue to be added to a phase (i.e. salty water) and continue to lower the freezing point.

What happens when too much salt is added to a solution?

Clearly, a solubility limit must exist and a new phase will appear.

This can be qualitatively understood by considering the behavior of the molar Gibbs free energy of forming a solution as a function of the amount of solute $X_B$:

To quantify the conditions for the appearance of new phases, consider the thermodynamics of binary (i.e. two component) alloys¹

The Gibbs-Duhem equation of a system consisting of two components $A$ and $B$ is:

$$0 = SdT - VdP + \sum N_i d\mu_i = SdT - VdP + N_A d\mu_A + N_B d\mu_B$$

Consider a closed system consisting of one mole of molecules: $N_A + N_B = 1$ mole:

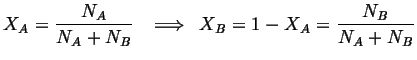$$\input{equations/20-3A}$$ (28-1)

The state of the system (per mole) should be representable by three independent parameters, $(T, P, X_B )$ or $(T, P, X_A)$. Therefore, using $\mu_A = \mu_A(P,T,X_B)$ and $\mu_B = \mu_B(P,T,X_B)$ in the Gibbs-Duhem equation:

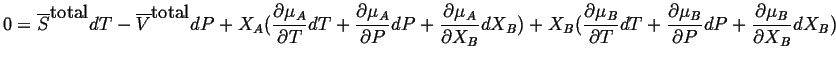$$\input{equations/20-4A}$$ (28-2)

where

$$d\mu_A = \ensuremath{\frac{\partial{\mu_A}}{\p... ...\partial{T}}}dP + \ensuremath{\frac{\partial{\mu_A}}{\partial{X_B}}}dX_B$$

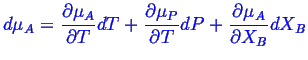
Note that $\ensuremath{\frac{\partial{\mu_A}}{\partial{T}}} = -\ensuremath{\overline{S_A}}$ and $\ensuremath{\frac{\partial{\mu_B}}{\partial{T}}} = \ensuremath{\overline{V_B}}$, thus,

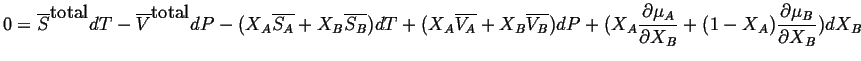$$\input{equations/20-4B}$$ (28-3)

The first and third terms cancel and the second and fourth terms cancel. Therefore,

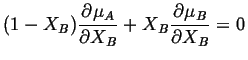$$\input{equations/20-4C}$$ (28-4)

This is a general result for binary solution. It is the form of the Gibbs-Duhem equation for solutions. Equation 28-4 gives a relation between the derivatives of the chemical potentials but not a relation between the chemical potentials themselves.