The Other Energy Functionals: The Legendre transformations

From Equation 21-1, the internal energy has the ``natural variables'' $U(S,V,N_i)$. To change to another set of natural variables, a new function is defined by subtracting off a particular conjugate pair:

For example: Enthalpy

$$\input{equations/leg-H}$$ (21-3)

For example: Helmholtz Free Energy

$$\input{equations/leg-F}$$ (21-4)

For example: Gibbs Free Energy

$$\input{equations/leg-G}$$ (21-5)

``The Legendre transformation'' is defined as the procedure of subtracting off conjugate pair to change that particular variable.

To see how the new variables appear, consider the Helmholtz free energy:

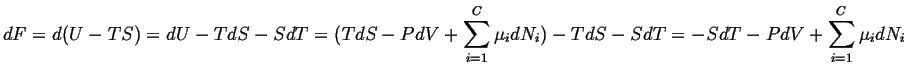$$\input{equations/15-2A}$$ (21-6)

implies

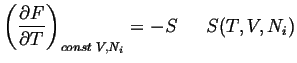$$\input{equations/15-2B}$$ (21-7)

Doing the same for $d(H) = d(U+PV)$

And for $d(G) = d(U - TS + PV)$

Trivial Example of a Legendre Transform

Suppose that the internal energy is composed of the thermal part plus a simple spring:

$$\begin{split}U(S,x) = TS + F x\\ = TS + \frac{k}{2} x^2 \end{split}$$ (21-8)

where

$$F(x) = \ensuremath{\frac{\partial{U}}{\partial{x}}}= kx$$ (21-9)

The Legendre transform from the $x$-variable to the $F$ variable is

$$\begin{split}\Phi = U(S,x) - F x\\ = TS + \frac{k}{2} x^2 - ... ...k}{2} x^2\\ = TS - \frac{1}{2k} F^2\\ = \Phi(S,F) \end{split}$$ (21-10)

It is fairly easy to show that the inverse Legendre transformation is simply $U = \Phi - (\partial \Phi/\partial F) F$.