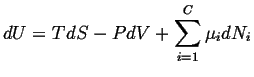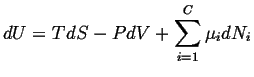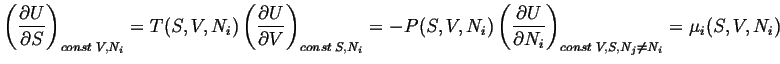

Next: The Other Energy Functionals:
Up: Lecture_21_web
Previous: Lecture_21_web
Our considerations of
equilibrium have produced some useful
results--these results are usually in the
form of some differential expression between quantities.
We will now consider some the useful mathematical
relations that follow from the combined form
of first and second law.
First
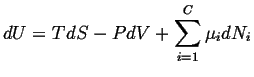 |
(21-1) |
This differential implies
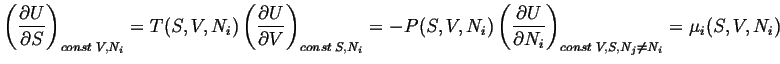 |
(21-2) |
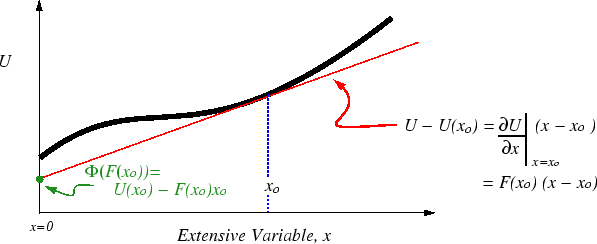
We can think of this equation as defining a
``rolling tangent plane''
Figure 21-1:
Illustration of a rolling tangent
plane in one dimension.
Evaluated at some arbitrary point 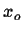 ,
the slope of the plane is the conjugate force to that variable,
,
the slope of the plane is the conjugate force to that variable, 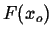 .
Using the equation of the tangent plane, we can define a new function.
.
Using the equation of the tangent plane, we can define a new function.
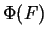 , which is the the intercept of the tangent plane with slope
, which is the the intercept of the tangent plane with slope 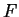 and the internal energy.
The value of the slopes of the tangent surface to
and the internal energy.
The value of the slopes of the tangent surface to 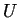 are related to the conjugate forces--the
values of these forces are in turn functions of where the tangent plane is placed.
In other words, the conjugate forces are also functions of the extensive variables.
are related to the conjugate forces--the
values of these forces are in turn functions of where the tangent plane is placed.
In other words, the conjugate forces are also functions of the extensive variables.
 |


Next: The Other Energy Functionals:
Up: Lecture_21_web
Previous: Lecture_21_web
W. Craig Carter
2002-10-25