

Next: About this document ...
Up: Lecture_21_web
Previous: The Other Energy Functionals:
Another important set of thermodynamics concepts fall under the
category of LeChatelier's principle. It is fundamentally an
easy idea, but for some reason it is taught in fairly confusing
ways.
The formal statement of LeChatelier's principle is something like
this:
|
``If a body at
equilibrium is disturbed by changing one of
its environment's variables, then the body's
internal variables will change so as to
mitigate the change in environment.''
|
This is a pretty confusing statement for something that
is fairly easy to understand.
Perhaps, the following statement is easier?
``If a stimulus would produce an effect of magnitude
1 in a material that is constrained not to change its
internal degrees of freedom, then an unconstrained
material would have a response that is less than
or equal to magnitude 1.''
No, not better? Oh, well.
Also, I've never found a good proof of this
which leads to any additional physical enlightenment, so I
won't disenlighten you by giving one (if you
want to get confused, see the discussion by Landau and
Lifshitz, Section 2.2; it is the best proof
that I know of).
I think it best to give a few examples.
- If the pressure is increased, the system
will find an equilibrium that decreases its
volume.
Remember our friendly ideal gas reaction:
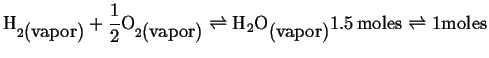 |
(21-11) |
If we increase pressure, will the composition favor the
reactants or products?
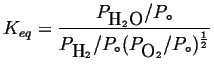 |
(21-12) |
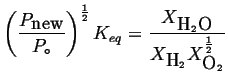 |
(21-13) |
- A crack in a material:
Figure 21-2:
A crack in a material--what is the response of
the material to an increased load?
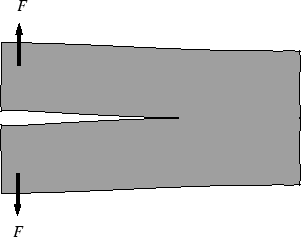 |
If the load is increased, the stiffness
decreases by propagating the crack.
Suppose that each homework set I give you is
about the same amount of work. You spend an
average of
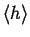 hours per problem. If
I were to assign ten times as many problems
this week
hours per problem. If
I were to assign ten times as many problems
this week
 would tend to decrease.
would tend to decrease.
One last note about LeChatelier's principle: it pertains
only for small changes applied to an equilibrium system that
is not near a condition of instability.
If a system is not in equilibrium, or the change in the
external conditions are very great, then we should not
expect LeChatelier's principle to apply.
As an example, consider a house with the
wind blowing past it. The wind blows the
door shut which seems like a violation of
LeChatelier's Principle.
Figure 21-3:
The stupid door doesn't care about
LeChatelier's principle.
 |
There is also the example of the ``Stupid Crack:''


Next: About this document ...
Up: Lecture_21_web
Previous: The Other Energy Functionals:
W. Craig Carter
2002-10-25
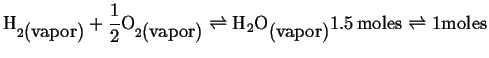
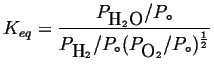
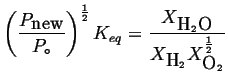
![]() hours per problem. If
I were to assign ten times as many problems
this week
hours per problem. If
I were to assign ten times as many problems
this week
![]() would tend to decrease.
would tend to decrease.

