Ludwig Boltzmann is credited with the discovery of microscopic definition
of entropy.
The definition is remarkably simple--however, it is not at all simple to
show that Boltzmann's microscopic definition of entropy is the same one
as we use in continuum thermodynamics:
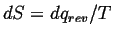 . .
Boltzmann's definition relates the entropy of a system to the number
of different ways that the system can store a fixed amount of
energy:
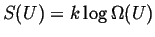 |
(16-4) |
where 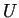 is the internal energy of a system and is the internal energy of a system and 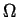 is the
number of distinguishable ways that the system can be arranged
with a fixed amount of internal energy.
The proportionality constant is the same one that relates
kinetic energy to temperature--it is called Boltzmann's constant
and is the ideal gas constant is the
number of distinguishable ways that the system can be arranged
with a fixed amount of internal energy.
The proportionality constant is the same one that relates
kinetic energy to temperature--it is called Boltzmann's constant
and is the ideal gas constant 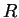 divided by Avogadro's number. divided by Avogadro's number.
One way to interpret equation 16-4 is that if an isolated
system (i.e., fixed 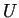 )
can undergo some change such that the number of states increases, it will
do so.
The interpretation of this is that if all observations are equally probable,
the state of the system with the most numerable observations is the
one that is most likely to be observed.
This is a slight change from our continuum definition of the second law
which stated that an observation of decreased universal entropy is
impossible.
The statistical mechanical definition says that an observation of
universal increased entropy is not probable. )
can undergo some change such that the number of states increases, it will
do so.
The interpretation of this is that if all observations are equally probable,
the state of the system with the most numerable observations is the
one that is most likely to be observed.
This is a slight change from our continuum definition of the second law
which stated that an observation of decreased universal entropy is
impossible.
The statistical mechanical definition says that an observation of
universal increased entropy is not probable.
Every course in statistical mechanics will have a section that demonstrates
out that--for all but the very smallest systems--the probability of
an observation of entropy decrease is so small that it virtually never
occurs.
Why should there be a logarithm in equation 16-4?
Remember that entropy is an extensive quantity.
The number of different states of two systems 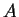 and and 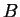 increase
when those state are considered together
is the product increase
when those state are considered together
is the product
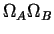 .1Therefore, if .1Therefore, if
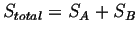 then a function is needed
that when the product of the number of states occurs then the
function is added.
The logarithm has this behavior: then a function is needed
that when the product of the number of states occurs then the
function is added.
The logarithm has this behavior:
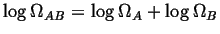 . . |
![]() -
-
![]() ) another degree of freedom arises which
relates to the ways that the system can be
mixed up. Entropy tends to decrease with
addition of a solute--this will be discussed when
we consider solutions.
) another degree of freedom arises which
relates to the ways that the system can be
mixed up. Entropy tends to decrease with
addition of a solute--this will be discussed when
we consider solutions.
