A Survey of Molar Entropies

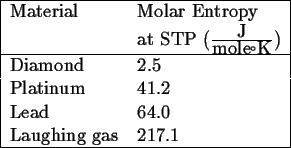
Consider the following data:

What do we observe; what correlations can we make?

Graphite is particularly illustrative of this point. Its molar entropy is in the same ballpark as diamond but higher. This correlates with its rigid bonds within the close-packed planes and weak van der Waals bounds out of plane.

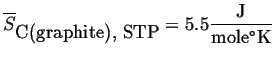$$\input{equations/103A}$$ (16-1)

Consider another list of data:

What observations or generalized can be made??

If a substance has several different forms (phases, crystal structures, etc.), then the higher entropy forms tend to be stable at high temperature (Note $\ensuremath{\overline{G}} = \ensuremath{\overline{H}} - T\ensuremath{\overline{S}}$, low $\ensuremath{\overline{G}}$ correlates with the more stable phases.

In other words, melting and evaporation tend to have positive changes in their entropy values. We already observed for H$_2$O:

The molar entropies rise with stability at higher temperature.

Wait a minute!

Vapor is not stable at STP! (Neither is ice . . . )

Question: How can we write down a number for something that isn't stable?

Consider our original enthalpy diagram:

Figure 16-2: Molar Enthalpies of solid, liquid, and vapor water as a function of temperature.

We extrapolate the enthalpy by fitting a curve for the heat capacity:

Figure 16-3: Extrapolating the Enthalpy by fitting a curve for the heat capacity.

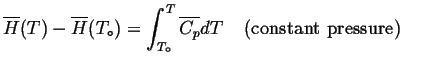$$\input{equations/106A}$$ (16-2)

Furthermore, we can use the definition of entropy to integrate the entropy so enthalpies are measured with regard to standard state.

Or, if it is known at some other state,

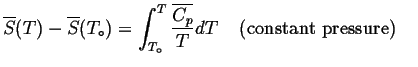$$\input{equations/106C}$$ (16-3)