A New Thermodynamic State Function: Enthalpy

For an simple pure fluid, consider the physical meaning of the $-PV$ term alone;

Question: What are the units of $PV$? What are the units of $P$?

Imagine that there is a completely homogeneous system that has been arbitrarilry divided into small volumes of size $dV$:

Figure 11-3: A uniformly homogeneous system (i.e. uniform pressure) of a simple pure fluid divided into an arbitrary of smaller systems of size $dV$

Consider what is left of the internal energy after we subtract off the ``mechanical'' or ``compression'' energy:

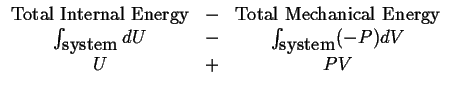$$\input{equations/enthalpy-integration}$$ (11-12)

The reason that the integration can be carried out is that both $dV$ and $dU$ are extensive variables and are thus additive for each subsystem.

So that we can define a new state function (that is also extensive),

$$\input{equations/enthalpy-legendre}$$ (11-13)

It is sensible to interpret $H$ as the ``thermal energy'' at constant pressure. In other words, we divide the internal energy for a simple fluid $U$ into two parts--one part corresponding to that stored as compressive energy ( $-PV$) and another part the thermal energy $H$. Another way to see this is:

$$\input{equations/75A}$$ (11-14)

In other words

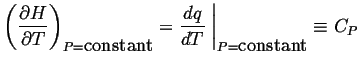$$\input{equations/Cp-enthalpy}$$ (11-15)

for an ideal gas:

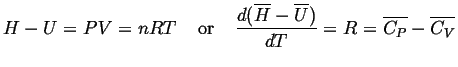$$\input{equations/enthalpy-IG}$$ (11-16)