We will show that the internal energy of
an ideal gas is a function of temperature
only.
This makes physical sense because there is an
assumption in ideal gas behavior that
there is no interaction between the molecules
when we write
![]()
Start with a reversible process for an ideal gas:
| (11-1) |
Consider two processes: one occurring at constant volume, the other occurring at constant pressure.
For process 1:
![]() ;
This can be integrated because
;
This can be integrated because
![]() is the only thing that is changing
on the righthandside (
is the only thing that is changing
on the righthandside (
![]() is assumed to be independent of
is assumed to be independent of
![]() and
and
![]() ).
).
For process 2:
![]() ;
;
![]() is constant (i.e., not a function of
is constant (i.e., not a function of
![]() or
or
![]() ) so it can be integrated directly.
Using the ideal gas law:
) so it can be integrated directly.
Using the ideal gas law:
| (11-2) |
So for process 2,
| (11-3) |
Since we can make up any quasi-static curve with segments
of
![]() processes and
processes and
![]() processes
processes
Evidently, the sum of any such processes is a
function only of
![]() . Therefore, for an ideal
gas
. Therefore, for an ideal
gas
| (11-4) |
Comparing the two equations:
| (11-5) |
| (11-6) |
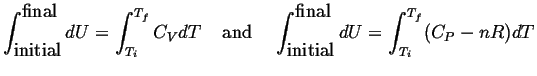 |
(11-7) |
| (11-8) |
| (11-9) |
| (11-10) |
or
| (11-11) |