Another State Function

Recall that $dq$ is not a perfect differential.

Let's consider $dq$ for an ideal gas undergoing a reversible process.

$$\input{equations/81A}$$ (11-17)

for an ideal gas

$$\input{equations/81B}$$ (11-18)

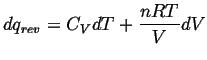$$\input{equations/81C}$$ (11-19)

Now divide through by $T$

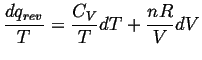$$\input{equations/81D}$$ (11-20)

Notice that we have separated the equation into something that is integrable over segments of $dT$ and $dV$ and thus over any curve.

Therefore, $dq_{rev}/{T}$ is a ``perfect differential'' and it must then be a state function for an ideal gas.